
【题目】已知椭圆![]() 的左焦点
的左焦点![]() 与抛物线
与抛物线![]() 的焦点重合,椭圆
的焦点重合,椭圆![]() 的离心率为
的离心率为![]() ,过点
,过点![]() 作斜率不为0的直线
作斜率不为0的直线![]() ,交椭圆
,交椭圆![]() 于
于![]() 两点,点
两点,点![]() ,且
,且![]() 为定值.
为定值.
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 面积的最大值.
面积的最大值.
【答案】(1) ![]() (2)
(2)![]()
【解析】试题分析:(1)由抛物线焦点可得c,再根据离心率可得a,即得b(2)先设直线方程x=ty+m,根据向量数量积表示![]() ,将直线方程与椭圆方程联立方程组,结合韦达定理代入化简可得
,将直线方程与椭圆方程联立方程组,结合韦达定理代入化简可得![]() 为定值的条件,解出m;根据点到直线距离得三角形的高,利用弦公式可得底,根据面积公式可得关于t的函数,最后根据基本不等式求最值
为定值的条件,解出m;根据点到直线距离得三角形的高,利用弦公式可得底,根据面积公式可得关于t的函数,最后根据基本不等式求最值
试题解析:解:(1)设F1(﹣c,0),∵抛物线y2=﹣4x的焦点坐标为(﹣1,0),且椭圆E的左焦点F与抛物线y2=﹣4x的焦点重合,∴c=1,
又椭圆E的离心率为![]() ,得a=
,得a=![]() ,
,
于是有b2=a2﹣c2=1.故椭圆Γ的标准方程为:![]() .
.
(2)设A(x1,y1),B(x2,y2),直线l的方程为:x=ty+m,
由![]() 整理得(t2+2)y2+2tmy+m2﹣2=0
整理得(t2+2)y2+2tmy+m2﹣2=0
,![]() ,
,
![]() ,
,
![]() =
=![]()
=(t2+1)y1y2+(tm﹣![]() t)(y1+y2)+m2﹣
t)(y1+y2)+m2﹣![]() =
= .
.
要使![]()
![]() 为定值,则
为定值,则 ,解得m=1或m=
,解得m=1或m=![]() (舍)
(舍)
当m=1时,|AB|=![]() |y1﹣y2|=
|y1﹣y2|=![]() ,
,
点O到直线AB的距离d=![]() ,
,
△OAB面积s=![]() =
= .
.
∴当t=0,△OAB面积的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴建立极坐标系,曲线
轴的正半轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 为曲线
为曲线![]() 上任意一点,求
上任意一点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
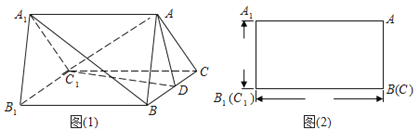
【题目】如图(1)是一个水平放置的正三棱柱![]() ,
, ![]() 是棱
是棱![]() 的中点.正三棱柱的正(主)视图如图(2).
的中点.正三棱柱的正(主)视图如图(2).
(Ⅰ)求正三棱柱![]() 的体积;
的体积;
(Ⅱ)证明: ![]() ;
;
(Ⅲ)图(1)中垂直于平面![]() 的平面有哪几个?(直接写出符合要求的平面即可,不必说明或证明)
的平面有哪几个?(直接写出符合要求的平面即可,不必说明或证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】地为绿化环境,移栽了银杏树![]() 棵,梧桐树
棵,梧桐树![]() 棵.它们移栽后的成活率分别
棵.它们移栽后的成活率分别
为![]() 、
、![]() ,每棵树是否存活互不影响,在移栽的
,每棵树是否存活互不影响,在移栽的![]() 棵树中:
棵树中:
(1)求银杏树都成活且梧桐树成活![]() 棵的概率;
棵的概率;
(2)求成活的棵树![]() 的分布列与期望.
的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的准线与
的准线与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 做圆
做圆![]() 的两条切线,切点为
的两条切线,切点为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() 是讲过定点
是讲过定点![]() 的一条直线,且与抛物线
的一条直线,且与抛物线![]() 交于
交于![]() 两点,过定点
两点,过定点![]() 作
作![]() 的垂线与抛物线交于
的垂线与抛物线交于![]() 两点,求四边形
两点,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取100名学生,测得他们的身高(单位: ![]() ),按照区间
),按照区间![]() ,
,
![]() 分组,得到样本身高的频率分布直方图(如图).
分组,得到样本身高的频率分布直方图(如图).

(1)求频率分布直方图中![]() 的值及身高在
的值及身高在![]() 以上的学生人数;
以上的学生人数;
(2)将身高在![]() 区间内的学生依次记为
区间内的学生依次记为![]() 三个组,用分层抽样的方法从这三个组中抽取6人,求从这三个组分别抽取的学生人数;
三个组,用分层抽样的方法从这三个组中抽取6人,求从这三个组分别抽取的学生人数;
(3)在(2)的条件下,要从6名学生中抽取2人.用列举法计算![]() 组中至少有1人被抽中的概率.
组中至少有1人被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点
的左焦点![]() 与抛物线
与抛物线![]() 的焦点重合,椭圆
的焦点重合,椭圆![]() 的离心率为
的离心率为![]() ,过点
,过点![]() 作斜率不为0的直线
作斜率不为0的直线![]() ,交椭圆
,交椭圆![]() 于
于![]() 两点,点
两点,点![]() ,且
,且![]() 为定值.
为定值.
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
极坐标系的极点为直角坐标系![]() 的原点,极轴为
的原点,极轴为![]() 轴的正半轴,两神坐标系中的长度单位相同.已知曲线
轴的正半轴,两神坐标系中的长度单位相同.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
, ![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)在曲线![]() 上求一点,使它到直线
上求一点,使它到直线![]() :
:  (
(![]() 为参数)的距离最短,写出
为参数)的距离最短,写出![]() 点的直角坐标.
点的直角坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com