练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆的右顶点、上顶点分别为A、B，坐标原点到直线AB的距离为，且.

    （1）求椭圆C的方程；

    （2）过椭圆C的左焦点的直线交椭圆于M、N两点，且该椭圆上存在点P，使得四边形MONP（图形上字母按此顺序排列）恰好为平行四边形，求直线的方程.

    【答案】（1）；（2）.

    【解析】

    （1）首先求直线方程，表示原点到直线的距离，再根据，联立解求椭圆方程；

    （2）直线，与椭圆方程联立，表示 ，，

    再利用中点坐标公式表示点的坐标，根据点在椭圆上，代入椭圆方程求

    (1) 设直线AB的方程为，

    原点到AB的距离为，又，

    解得，

    故椭圆的方程为；

    （2）由（1）得椭圆的左焦点，

    易知直线的斜率不为0，可设直线，设，

    因为MOPN为平行四边形，

    得 ，

    联立，

    ，

    因为点P在椭圆上，有

    所以直线的方程为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）讨论的单调性；

    （2）是否存在，，使得函数在区间的最小值为且最大值为？若存在，求出，的所有值；若不存在，请说明理由.

    参考数据：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司决定投人资金进行产品研发以提高产品售价.已知每件产品的制造成本为元，若投人的总的研发成本(万元)与每件产品的销售单价(元)的关系如下表:

    （1）求关于的线性回归方程;

    （2）市场部发现，销售单价(元)与销量(件)存在以下关系：，.根据（1）中结果预测，当为何值时，可获得最高的利润？

    附:，.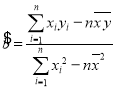

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图,某城市中心花园的边界是圆心为O,直径为1千米的圆,花园一侧有一条直线型公路l,花园中间有一条公路AB(AB是圆O的直径),规划在公路l上选两个点P,Q,并修建两段直线型道路PB,QA.规划要求:道路PB,QA不穿过花园.已知,(CD为垂足),测得OC=0.9,BD=1.2(单位:千米).已知修建道路费用为m元/千米.在规划要求下,修建道路总费用的最小值为_____元.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}为等差数列,a1=1,前n项和为Sn,数列{bn}为等比数列,b1>1,公比为2,且b2S3=54,b3+S2=16.

    (Ⅰ)求数列{an}与{bn}的通项公式;

    (Ⅱ)设数列{cn}满足cn=an+bn,求数列{cn}的前n项和Tn.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝ln (x＋1)－ －x，a∈R.

    (1)当a>0时，求函数f(x)的单调区间；

    (2)若存在x>0，使f(x)＋x＋1<－ (a∈Z)成立，求a的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知在等比数列{an}中，＝2，，＝128，数列{bn}满足b1＝1，b2＝2，且{}为等差数列．

    （1）求数列{an}和{bn}的通项公式；

    （2）求数列{bn}的前n项和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某工厂生产一批零件，为了解这批零件的质量状况，检验员从这批产品中随机抽取了100件作为样本进行检测，将它们的重量（单位：g）作为质量指标值．由检测结果得到如下频率分布直方图．

    分组

    频数

    频率

    8

    16

    0.16

    4

    0.04

    合计

    100

    1

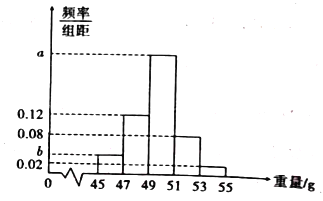
    （1）求图中的值；

    （2）根据质量标准规定：零件重量小于47或大于53为不合格品，重量在区间和内为合格品，重量在区间内为优质品．已知每件产品的检测费用为5元，每件不合格品的回收处理费用为20元．以抽检样本重量的频率分布作为该零件重量的概率分布．若这批零件共件，现有两种销售方案：方案一：不再检测其他零件，整批零件除对已检测到的不合格品进行回收处理，其余零件均按150元/件售出；方案二：继续对剩余零件的重量进行逐一检测，回收处理所有不合格品，合格品按150元/件售出，优质品按200元/件售出．仅从获得利润大的角度考虑，该生产商应选择哪种方案？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知是椭圆的左焦点，且椭圆经过点.

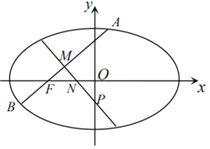
    （Ⅰ）求椭圆的方程；

    （Ⅱ）若过点的直线交椭圆于、两点，线段的中点为，过且与垂直的直线与轴和轴分别交于、两点，记、的面积分别为、．若，求直线的方程．

    查看答案和解析>>

    同步练习册答案