
【题目】已知函数![]() 是定义域为
是定义域为![]() 的奇函数,当
的奇函数,当![]() .
.
(Ⅰ)求出函数![]() 在
在![]() 上的解析式;
上的解析式;
(Ⅱ)在答题卷上画出函数![]() 的图象,并根据图象写出
的图象,并根据图象写出![]() 的单调区间;
的单调区间;

(Ⅲ)若关于![]() 的方程
的方程![]() 有三个不同的解,求
有三个不同的解,求![]() 的取值范围。
的取值范围。
科目:高中数学 来源: 题型:
【题目】为了了解初三学生女生身高情况,某中学对初三女生身高进行了一次测量,所得数据整理后列出了频率分布表如下:
组 别 | 频数 | 频率 |
[145.5,149.5) | 1 | 0.02 |
[149.5,153.5) | 4 | 0.08 |
[153.5,157.5) | 20 | 0.40 |
[157.5,161.5) | 15 | 0.30 |
[161.5,165.5) | 8 | 0.16 |
[165.5,169.5) | m | n |
合 计 | M | N |

(1)求出表中![]() 所表示的数;
所表示的数;
(2)画出频率分布直方图;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:如图,梯形ABCD中,AD∥BC,∠C= ![]() ,以AB为直径的⊙O恰与CD相切于点E,⊙O交BC于F,连结EF.
,以AB为直径的⊙O恰与CD相切于点E,⊙O交BC于F,连结EF. 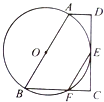
(1)求证:AD+BC=AB;
(2)求证:EF是AD与AB的等比中项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x+log2x+b在区间( ![]() ,4)上有零点,则实数b的取值范围是( )
,4)上有零点,则实数b的取值范围是( )
A.(﹣10,0)
B.(﹣8,1)
C.(0,10)
D.(1,12)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 对一切实数
对一切实数![]() 都有
都有![]()
![]() 成立,且
成立,且![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的解析式;
的解析式;
(3)已知![]() ,设
,设![]() :当
:当![]() 时,不等式
时,不等式![]() 恒成立;Q:当
恒成立;Q:当![]() 时,
时,![]() 是单调函数。如果满足
是单调函数。如果满足![]() 成立的
成立的![]() 的集合记为
的集合记为![]() ,满足Q成立的
,满足Q成立的![]() 的集合记为
的集合记为![]() ,求A∩(CRB)(
,求A∩(CRB)(![]() 为全集).
为全集).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小学为迎接校运动会的到来,在三年级招募了16名男志愿者和14名女志愿者.调查发现,男、女志愿者中分别各有10人和6人喜欢运动,其余人员不喜欢运动.
(1)根据以上数据完成2×2列联表,并说明是否有95%的把握认为性别与喜欢运动有关;
喜欢运动 | 不喜欢运动 | 总计 | |
男 | |||
女 | |||
总计 |
(2)如果喜欢运动的女志愿者中恰有4人懂得医疗救护,现从喜欢运动的女志愿者中抽取2名负责处理应急事件,求抽出的2名志愿者都懂得医疗救护的概率.
附:K2= ,
,
P(K2≥k0) | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com