练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知圆.

    （1）若不经过坐标原点的直线与圆相切，且直线在两坐标轴上的截距相等，求直线的方程；

    （2）设点在圆上，求点到直线距离的最大值与最小值.

    【答案】（1）或；（2）和.

    【解析】

    试题分析：（1）把圆的方程化为标准,找出圆心坐标和半径,根据直线在两坐标轴上的截距相等且不经过坐标原点设出直线的方程为,利用点到直线的距离公式求出圆心到直线的距离,让距离等于半径列出关于的方程,求出方程的解即可得到的值,进而确定出直线的方程；（2）利用点到直线的距离公式求出圆心到直线 的距离,所以点到直线距离的最大，小值为和.

    试题解析：（1）圆的方程可化为，即圆心的坐标为，半径为，因为直线在两坐标轴上的截距相等且不经过坐标原点，所以可设直线的方程为；于是有，得或，因此直线的方程为或.

    （2）因为圆心到直线的距离为，

    所以点到直线距离的最大值与最小值依次分别为 和.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】为推行“新课堂”教学法，某化学老师分别用传统教学和“新课堂”两种不同的教学方式，在甲、乙两个平行班级进行教学实验，为了比较教学效果，期中考试后，分别从两个班级中各随机抽取20名学生的成绩进行统计，作出的茎叶图如下图：记成绩不低于70分者为“成绩优良”.

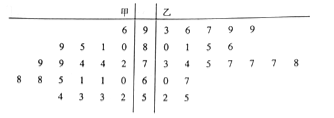
    （1）分别计算甲、乙两班20个样本中，化学分数前十的平均分，并大致判断哪种教学方式的教学效果更佳；

    （2）由以上统计数据填写下面列联表，并判断能否在犯错误的概率不超过的前提下认为“成绩优良与教学方式有关”？

    甲班

    乙班

    总计

    成绩优良

    成绩不优良

    总计

    附：

    独立性检验临界值表：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某研究型学习小组调查研究学生使用智能手机对学习的影响．部分统计数据如下表：

    使用智能手机

    不使用智能手机

    总计

    学习成绩优秀

    4

    8

    12

    学习成绩不优秀

    16

    2

    18

    总计

    20

    10

    30

    附表：

    P(K2≥k0)

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    k0

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    经计算的观测值为10，则下列选项正确的是(　　)

    A. 有99.5%的把握认为使用智能手机对学习有影响

    B. 有99.5%的把握认为使用智能手机对学习无影响

    C. 在犯错误的概率不超过0.001的前提下认为使用智能手机对学习有影响

    D. 在犯错误的概率不超过0.001的前提下认为使用智能手机对学习无影响

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某研究型学习小组调查研究学生使用智能手机对学习的影响．部分统计数据如下表：

    使用智能手机

    不使用智能手机

    总计

    学习成绩优秀

    4

    8

    12

    学习成绩不优秀

    16

    2

    18

    总计

    20

    10

    30

    附表：

    P(K2≥k0)

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    k0

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    经计算的观测值为10，则下列选项正确的是(　　)

    A. 有99.5%的把握认为使用智能手机对学习有影响

    B. 有99.5%的把握认为使用智能手机对学习无影响

    C. 在犯错误的概率不超过0.001的前提下认为使用智能手机对学习有影响

    D. 在犯错误的概率不超过0.001的前提下认为使用智能手机对学习无影响

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某城市一汽车出租公司为了调查A，B两种车型的出租情况，现随机抽取了这两种车型各100辆，分别统计了每辆车某个星期内的出租天数，统计数据如下表：

    A车型 B车型

    出租天数

    1

    2

    3

    4

    5

    6

    7

    出租天数

    1

    2

    3

    4

    5

    6

    7

    车辆数

    5

    10

    30

    35

    15

    3

    2

    车辆数

    14

    20

    20

    16

    15

    10

    5

    （Ⅰ）从出租天数为3天的汽车（仅限A，B两种车型）中随机抽取一辆，估计这辆汽车恰好是A型车的概率；

    （Ⅱ）根据这个星期的统计数据，估计该公司一辆A型车，一辆B型车一周内合计出租天数恰好为4天的概率；

    （Ⅲ）

    （ⅰ）试写出A，B两种车型的出租天数的分布列及数学期望；

    （ⅱ）如果两种车辆每辆车每天出租获得的利润相同，该公司需要从A，B两种车型中购买一辆（注：两种车型的采购价格相当），请你根据所学的统计知识，建议应该购买哪一种车型，并说明你的理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】椭圆的中心在坐标原点，焦点在轴上，焦点到短轴端点的距离为2，离心率为.

    （Ⅰ）求该椭圆的方程；

    （Ⅱ）若直线与椭圆交于， 两点且，是否存在以原点为圆心的定圆与直线相切？若存在求出定圆的方程；若不存在，请说明理由

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，求在区间上的最值；

    （2）讨论函数的单调性；

    （3）当时，有恒成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，动点到定点的距离和它到直线的距离

    之比是常数，记动点的轨迹为.

    （1）求轨迹的方程；

    （2）过点且不与轴重合的直线，与轨迹交于,两点，线段的垂直平分线与轴交于点，与轨迹是否存在点，使得四边形为菱形？若存在，请求出直线的方程；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知a，b为常数，且a≠0，f(x)＝ax2＋bx，f(2)＝0，方程f(x)＝x有两个相等实数根．

    (1)求函数f(x)的解析式；

    (2)当x∈[1,2]时，求f(x)的值域；

    (3)若F(x)＝f(x)－f(－x)，试判断F(x)的奇偶性，并证明你的结论．

    查看答案和解析>>

    同步练习册答案