
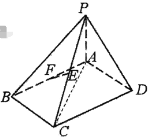
【题目】如图,四棱锥P-ABCD中,底面ABCD为菱形,![]() 底面ABCD,
底面ABCD,![]() ,
,![]() ,E、F分别是PC和AB的中点.
,E、F分别是PC和AB的中点.
(1)证明:![]() 平面PAD;
平面PAD;
(2)若![]() ,求PD与平面PBC所成角的正弦值.
,求PD与平面PBC所成角的正弦值.
【答案】(1)证明见详解;(2)![]()
【解析】
(1)在平面PAD中寻找EF的平行线,由线线平行,推证线面平行即可;
(2)根据题意,建立空间直角坐标系,通过向量法求解.
(1)取PD中点为M,根据题意作图如下:
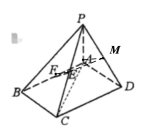
因为E、M均为三角形PCD中两边中点,
则![]() ,且
,且![]() ,
,
而![]() ,
,![]() ,
,
故AF//EM,且AF=EM,
则四边形AMEF为平行四边形.
故![]() .
.
又EF不在面PAD,![]() 面PAD,
面PAD,
故![]() 面PAD.
面PAD.
(2)由题设知![]() 底面ABCD,
底面ABCD,
故PA![]()
![]() ,又
,又![]() ,故
,故![]() 平面PAB
平面PAB
因为![]() //AD,
//AD,
故![]() 平面PAB
平面PAB
又![]() 面PAB
面PAB
则AD![]() AB
AB
综上所述:![]() AD
AD![]() AB
AB
且菱形ABCD为正方形,由AC=4,
解得正方形ABCD的边长为![]() .
.
以A为坐标原点,过点A,作BD的平行线为![]() 轴,
轴,
建立如图空间直角坐标系![]() ,
,
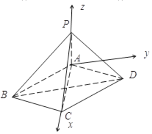
则![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
设平面PBC的法向量为![]() ,则
,则
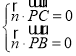 ,即
,即![]()
取![]() ,又
,又![]()
设PD与平面PBC所成角为![]() ,则
,则
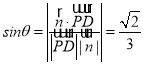 .
.
故直线PD与平面PBC所成角的正弦值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,用![]() 种不同的颜色给图中的
种不同的颜色给图中的![]() 个格子涂色,每个格子涂一种颜色,要求最多使用
个格子涂色,每个格子涂一种颜色,要求最多使用![]() 种颜色且相邻的两个格子颜色不同,则不同的涂色方法共有( )
种颜色且相邻的两个格子颜色不同,则不同的涂色方法共有( )
A.![]() 种B.
种B.![]() 种C.
种C.![]() 种D.
种D.![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.若![]() 为真命题,则
为真命题,则![]() ,
,![]() 均为假命题;
均为假命题;
B.命题“若![]() ,则
,则![]() ”的逆否命题为真命题;
”的逆否命题为真命题;
C.等比数列![]() 的前
的前![]() 项和为
项和为![]() ,若“
,若“![]() ”则“
”则“![]() ”的否命题为真命题;
”的否命题为真命题;
D.“平面向量![]() 与
与![]() 的夹角为钝角”的充要条件是“
的夹角为钝角”的充要条件是“![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着手机的发展,“微信”逐渐成为人们交流的一种形式,某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如表:
年龄(单位:岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(1)若以“年龄55岁为分界点”,由以上统计数据完成下面![]() 列联表,并判断是否有99.9%的把握认为“使用微信交流”的态度与人的年龄有关;
列联表,并判断是否有99.9%的把握认为“使用微信交流”的态度与人的年龄有关;
年龄不低于55岁的人数于 | 年龄低于55岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(2)若从年龄在![]() 的被调查人中随机选取2人进行追踪调查,求2人中至少有1人赞成“使用微信交流”的概率.
的被调查人中随机选取2人进行追踪调查,求2人中至少有1人赞成“使用微信交流”的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)已知某班共有![]() 人,记这
人,记这![]() 人生日至少有两人相同的概率为
人生日至少有两人相同的概率为![]() ,
,![]() ,将一年看作365天.
,将一年看作365天.
(i)求![]() 的表达式;
的表达式;
(ii)估计![]() 的近似值(精确到0.01).
的近似值(精确到0.01).
参考数值:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 1(a>b>0),椭圆C上的点到焦点距离的最大值为9,最小值为1.
1(a>b>0),椭圆C上的点到焦点距离的最大值为9,最小值为1.
(1)求椭圆C的标准方程;
(2)求椭圆C上的点到直线l:4x﹣5y+40=0的最小距离?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:x2=4y的焦点为F,过点P(-2,2)的直线l与抛物线C交于A,B两点.
(1)当点P为A、B的中点时,求直线AB的方程;
(2)求|AF||BF|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 的圆心为
的圆心为![]() ,直线
,直线![]() 过点
过点![]() 且与
且与![]() 轴不重合,交圆
轴不重合,交圆![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() .
.
(1)求![]() 的值;
的值;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,与直线
两点,与直线![]() 相交于
相交于![]() 点,试问在椭圆
点,试问在椭圆![]() 上是否存在一定点
上是否存在一定点![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等差数列(其中
成等差数列(其中![]() ,
,![]() ,
,![]() 分别指直线
分别指直线![]() ,
,![]() ,
,![]() 的斜率).若存在,求出
的斜率).若存在,求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(卷号)2040818101747712
(题号)2050752239689728
(题文)
在平面直角坐标系中,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系.已知直线![]() 的参数方程为
的参数方程为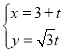 (
(![]() 为参数),曲线C的极坐标方程为
为参数),曲线C的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,点
两点,点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com