
���� ��1����Ȳ�����{an}�Ĺ���Ϊd��{bn}�ǵȱ����У��蹫��Ϊq�����õȲ����к͵ȱ����е�ͨ�ʽ���ⷽ�̿ɵ������������õ������ͨ�ʽ��
��2�����cn���������е���ͷ���������������ͺʹ�λ����������ɵõ�����ͣ�
��� �⣺��1����Ȳ�����{an}�Ĺ���Ϊd��{bn}�ǵȱ����У��蹫��Ϊq��
������ɵ�q+6+d=10��3+4d-2q=3+2d��
���d=q=2��
������{an}��ͨ��Ϊan=a1+��n-1��d=3+2��n-1��=2n+1��
��{bn}��ͨ��Ϊbn=b1qn-1=2n-1��
��2��cn=$\left\{\begin{array}{l}{\frac{2}{{S}_{n}}��nΪ����}\\{{a}_{n}{b}_{n}��nΪż��}\end{array}\right.$=$\left\{\begin{array}{l}{\frac{2}{n��n+2��}��nΪ����}\\{��2n+1��•{2}^{n-1}��nΪż��}\end{array}\right.$��
��T2n=[$\frac{2}{1��3}$+$\frac{2}{3��5}$+��+$\frac{2}{��2n-1����2n+1��}$]+[5•2+9•23+��+��4n+1��•22n-1]��
��S=$\frac{2}{1��3}$+$\frac{2}{3��5}$+��+$\frac{2}{��2n-1����2n+1��}$=1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+��+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$
=1-$\frac{1}{2n+1}$=$\frac{2n}{2n+1}$��
��T=5•2+9•23+��+��4n+1��•22n-1��
4T=5•8+9•25+��+��4n+1��•22n+1��
��ʽ����ɵ�-3T=10+4��8+32+��+22n-1��-��4n+1��•22n+1
=10+4•$\frac{8��1-{4}^{n-1}��}{1-4}$-��4n+1��•22n+1��
����ɵã�T=$\frac{2-��1-12n��•{2}^{2n+1}}{9}$��
����T2n=$\frac{2n}{2n+1}$+$\frac{2-��1-12n��•{2}^{2n+1}}{9}$��
���� ���⿼��Ȳ����к͵ȱ����е�ͨ�ʽ�����ʽ�����ã��������е���ͷ���������������ʹ�λ��������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ��ڶ����� | B�� | ��һ��������� | C�� | �ڶ���������� | D�� | ���Ļ�������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{5}$-1 | B�� | 2$+\sqrt{5}$ | C�� | 3$+\sqrt{5}$ | D�� | 5$+\sqrt{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���ڵ㣨$\frac{��}{4}$��0�����ĶԳ� | B�� | ���ڵ㣨$\frac{��}{2}$��0�����ĶԳ� | ||
| C�� | ���ڵ㣨$\frac{3��}{4}$��0�����ĶԳ� | D�� | ���ڵ㣨�У�0�����ĶԳ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
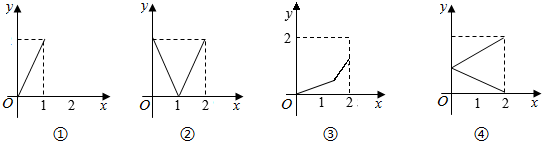
| A�� | �٢� | B�� | �ڢ� | C�� | �ۢ� | D�� | �٢� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com