
【题目】△ABC的外接圆半径R= ![]() ,角A,B,C的对边分别是a,b,c,且
,角A,B,C的对边分别是a,b,c,且 ![]() =
= ![]()
(1)求角B和边长b;
(2)求S△ABC的最大值及取得最大值时的a,c的值,并判断此时三角形的形状.
【答案】
(1)解:∵ ![]() ,
,
∴2sinAcosB﹣sinCcosB=sinBcosC,可得2sinAcosB=sinBcosC+cosBsinC=sin(B+C),
∵在△ABC中,sin(B+C)=sin(π﹣A)=sinA>0,
∴2sinAcosB=sinA,可得cosB= ![]() .
.
又∵B∈(0,π),∴ ![]() ,
,
由正弦定理 ![]() ,可得b=2RsinB=2
,可得b=2RsinB=2 ![]() sin
sin ![]() =3
=3
(2)解:∵b=3, ![]() ,
,
∴由余弦定理b2=a2+c2﹣2accosB,得a2+c2﹣ac=9,
因此,ac+9=a2+c2≥2ac,可得ac≤9,当且仅当a=c时等号成立,
∵S△ABC= ![]() =
= ![]() ,∴
,∴ ![]()
由此可得:当且仅当a=c时,S△ABC有最大值 ![]() ,此时a=b=c=3,可得△ABC是等边三角形
,此时a=b=c=3,可得△ABC是等边三角形
【解析】(1)运用两角和的正弦公式将已知等式化简整理,得到2sinAcosB=sin(B+C),根据三角函数的诱导公式可得sin(B+C)=sinA>0,从而得出cosB= ![]() ,可得
,可得 ![]() ,最后由正弦定理加以计算,可得边b的长;(2)由b=3且
,最后由正弦定理加以计算,可得边b的长;(2)由b=3且 ![]() ,利用余弦定理算出a2+c2﹣ac=9,再根据基本不等式算出ac≤9.利用三角形的面积公式算出S△ABC=
,利用余弦定理算出a2+c2﹣ac=9,再根据基本不等式算出ac≤9.利用三角形的面积公式算出S△ABC= ![]() ,从而得到当且仅当a=c时,S△ABC有最大值
,从而得到当且仅当a=c时,S△ABC有最大值 ![]() ,进而得到此时△ABC是等边三角形.
,进而得到此时△ABC是等边三角形.


科目:高中数学 来源: 题型:
【题目】图中程序是计算2+3+4+5+6的值的程序.在WHILE后的①处和在s=s+i之后的②处所就填写的语句可以是( )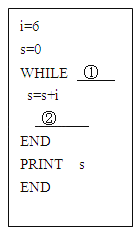
A.①i>1②i=i﹣1
B.①i>1②i=i+1
C.①i>=1②i=i+1
D.①i>=1②i=i﹣1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对的边分别为a,b,c,且c=2,C=60°.
(1)求 ![]() 的值;
的值;
(2)若a+b=ab,求△ABC的面积S△ABC .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C所对的边分别为a,b,c,已知a=2,b=3,cosC= ![]() .
.
(1)求△ABC的面积;
(2)求sin(C﹣A)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体ABCD﹣A1B1C1D1中,B1 C和C1D与底面A1B1C1D1所成的角分别为60°和45°,则异面直线B1C和C1D所成角的余弦值为( ) 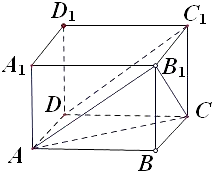
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点, ![]() 轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线
轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)设![]() 为参数,若
为参数,若![]() ,求直线
,求直线![]() 的参数方程;
的参数方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,设
,设![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com