
分析 (1)由f(x)在R上为奇函数,可得f(0)=0,再由x<0,-x>0,f(x)=-f(-x),即可得到所求解析式,画出分段函数的图象;
(2)由f(x)在R上为奇函数,且为增函数,可得t2-2t<-k+2t2,再由参数分离和二次函数的最值的求法,即可得到所求k的范围.
解答 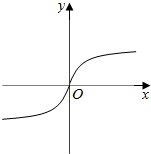 解:(1)∵f(x)为定义在R上的奇函数,
解:(1)∵f(x)为定义在R上的奇函数,
∴f(0)=0,
x<0时,-x>0,当x>0时,f(x)=lg(x+1)
则f(x)=-f(-x)=-lg(-x+1),
综上,$f(x)=\left\{\begin{array}{l}lg(x+1),x>0\\ 0,x=0\\-lg(-x+1),x<0\end{array}\right.$;
f(x)的大致图象为右图;
(2)由(1)可知f(x)在R上为增函数,
f(t2-2t)+f(k-2t2)<0⇒f(t2-2t)<-f(k-2t2)
⇒f(t2-2t)<f(-k+2t2)⇒t2-2t<-k+2t2⇒k<t2+2t恒成立,
由t2+2t=(t+1)2-1≥-1,⇒k<-1,
所以k的取值范围是(-∞-1).
点评 本题考查函数的奇偶性和单调性的判断和运用,考查不等式恒成立问题的解法,注意运用参数分离和二次函数的最值的求法,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{8}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3e | B. | -1 | C. | -e3 | D. | e2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1080 | B. | 480 | C. | 1560 | D. | 300 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{{a}^{2}-{x}^{2}}}{a}$ | B. | $\frac{1}{2}$(a2-x2)${\;}^{\frac{3}{2}}$ | C. | x(a2-x2)${\;}^{-\frac{3}{2}}$ | D. | -$\frac{1}{2}$(a2-x2)${\;}^{\frac{3}{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com