
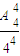 =
=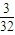 .
.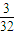 .
.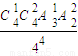 =
=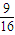 .
. .
.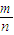 .解决此类问题,还需要考试熟练运用排列、组合的知识,并能准确求出公式中的n,m的值.
.解决此类问题,还需要考试熟练运用排列、组合的知识,并能准确求出公式中的n,m的值. 

科目:高中数学 来源:上海交通大学附属中学2012届度高二下学期期末考试数学 题型:填空题
把4个不同的球任意投入4个不同的盒子内(每盒装球数不限),则无空盒的概率为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com