
【题目】已知数列 ![]() 中,
中, ![]() .
.
(1)求证:数列 ![]() 与
与 ![]() 都是等比数列;
都是等比数列;
(2)若数列 ![]() 的前
的前 ![]() 项和为
项和为 ![]() .令
.令 ![]() ,求数列
,求数列 ![]() 的最大项.
的最大项.
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)一个盒子里装有三张卡片,分别标记有数字![]() ,
,![]() ,
,![]() ,这三张卡片除标记的数字外完全相同。随机有放回地抽取
,这三张卡片除标记的数字外完全相同。随机有放回地抽取![]() 次,每次抽取
次,每次抽取![]() 张,将抽取的卡片上的数字依次记为
张,将抽取的卡片上的数字依次记为![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求“抽取的卡片上的数字满足![]() ”的概率;
”的概率;
(Ⅱ)求“抽取的卡片上的数字![]() ,
,![]() ,
,![]() 不完全相同”的概率.
不完全相同”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)当a>0时,解关于x的不等式f(x)<0;
(2)若当a>0时,f(x)<0在x ![]() [1,2]上恒成立,求实数a的取值范围.
[1,2]上恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
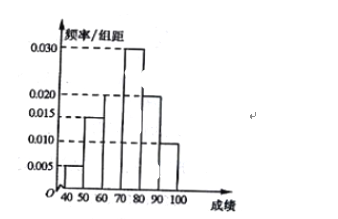
【题目】某中学举行了数学测试,并从中随机抽取了60名学生的成绩(满分100分)作为样本,其中成绩不低于80分的学生被评为优秀生,得到成绩分布的频率分布直方图如图所示.
(I)若该所中学共有3000名学生,试利用样本估计全校这次考试中优秀生人数;
(II)若在样本中,利用分层抽样的方法从成绩不低于70分的学生中随机抽取6人,再从中抽取3人,试求恰好抽中1名优秀生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列 ![]() 有无穷项,且每一项均为自然数,若75,99,235为
有无穷项,且每一项均为自然数,若75,99,235为 ![]() 中的项,则下列自然数中一定是
中的项,则下列自然数中一定是 ![]() 中的项的是( )
中的项的是( )
A.2017
B.2019
C.2021
D.2023
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
如图,在四棱锥P—ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=![]() ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
(Ⅰ)求证:PO⊥平面ABCD;
(Ⅱ)求异面直线PB与CD所成角的余弦值;
(Ⅲ)求点A到平面PCD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的右焦点为
的右焦点为 ![]() ,且点
,且点 ![]() 在椭圆
在椭圆 ![]() 上.
上.
(1)求椭圆 ![]() 的标准方程;
的标准方程;
(2)过椭圆 ![]() 上异于其顶点的任意一点
上异于其顶点的任意一点 ![]() 作圆
作圆 ![]() 的两条切线,切点分别为
的两条切线,切点分别为 ![]() (
( ![]() 不在坐标轴上),若直线
不在坐标轴上),若直线 ![]() 在
在 ![]() 轴,
轴, ![]() 轴上的截距分别为
轴上的截距分别为 ![]() ,证明:
,证明: ![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com