
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() (
(![]() )的左右两个焦点分别是
)的左右两个焦点分别是![]() 、
、![]() ,
,![]() 在椭圆
在椭圆![]() 上运动.
上运动.
(1)若对![]() 有最大值为120°,求出
有最大值为120°,求出![]() 、
、![]() 的关系式;
的关系式;
(2)若点![]() 是在椭圆上位于第一象限的点,过点
是在椭圆上位于第一象限的点,过点![]() 作直线
作直线![]() 的垂线
的垂线![]() ,过
,过![]() 作直线
作直线![]() 的垂线
的垂线![]() ,若直线
,若直线![]() 、
、![]() 的交点
的交点![]() 在椭圆
在椭圆![]() 上,求点
上,求点![]() 的坐标;
的坐标;
(3)若设![]() ,在(2)成立的条件下,试求出
,在(2)成立的条件下,试求出![]() 、
、![]() 两点间距离的函数
两点间距离的函数![]() ,并求出
,并求出![]() 的值域.
的值域.
【答案】(1)![]() ;(2)
;(2) ;(3)
;(3)![]() ,
,![]() 的值域为
的值域为![]() .
.
【解析】
(1)根据椭圆定义可知![]() ,再利用余弦定理及基本不等式可得
,再利用余弦定理及基本不等式可得![]() 的关系式;
的关系式;
(2)设出![]() 点坐标,分别求出直线
点坐标,分别求出直线![]() 与直线
与直线![]() 的方程,结合
的方程,结合![]() 在椭圆上即可求得点
在椭圆上即可求得点![]() 的坐标;
的坐标;
(3)把![]() 的坐标用含有
的坐标用含有![]() 的代数式表示,由两点间的距离公式可得两点
的代数式表示,由两点间的距离公式可得两点![]() 间距离的函数
间距离的函数![]() ,再换元由单调性求出其值域.
,再换元由单调性求出其值域.
(1) 根据椭圆的定义可知,![]() ,
,![]() ,
,
因为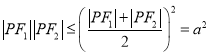
所以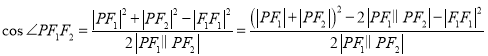
![]()
![]() ,即
,即![]() .
.
(2)设![]() ,
,![]()
当![]() 时,直线
时,直线![]() 斜率不存在,易知
斜率不存在,易知![]() 与
与![]() 重合,不满足题意;
重合,不满足题意;
当![]() 时,则直线
时,则直线![]() 的斜率
的斜率![]() ,直线
,直线![]() 的斜率
的斜率![]() ,
,
直线![]() 的方程
的方程![]() ,①
,①
直线![]() 的斜率
的斜率![]() ,则直线
,则直线![]() 的斜率
的斜率![]() ,
,
直线![]() 的方程
的方程![]() ,②
,②
联立①②,解得: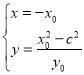 ,则
,则![]() ,
,
由![]() 在椭圆上,
在椭圆上,![]() 的横坐标互为相反数,纵坐标应相等,则
的横坐标互为相反数,纵坐标应相等,则![]() ,
,
![]() ,
,
则 ,又
,又![]() 在第一象限,
在第一象限,![]() 的坐标为
的坐标为![]() ;
;
(3)若![]() ,则
,则![]() ,
,![]() ,
,
则![]() ,
,![]() .
.
令![]() ,则
,则![]() ,
,
![]() ,
,![]() 在
在![]() 上为增函数,
上为增函数,
![]() 的值域为
的值域为![]() ,
,
即![]() 的值域为
的值域为![]() .
.


科目:高中数学 来源: 题型:
【题目】某市政府为减轻汽车尾气对大气的污染,保卫蓝天,鼓励广大市民使用电动交通工具出行,决定为电动车(含电动自行车和电动汽车)免费提供电池检测服务.现从全市已挂牌照的![]() 电动车中随机抽取100辆委托专业机构免费为它们进行电池性能检测,电池性能分为需要更换、尚能使用、较好、良好四个等级,并分成电动自行车和电动汽车两个群体分别进行统计,样本分布如图.
电动车中随机抽取100辆委托专业机构免费为它们进行电池性能检测,电池性能分为需要更换、尚能使用、较好、良好四个等级,并分成电动自行车和电动汽车两个群体分别进行统计,样本分布如图.
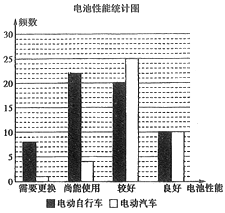
(1)采用分层抽样的方法从电池性能较好的电动车中随机抽取9辆,再从这9辆中随机抽取2辆,求至少有一辆为电动汽车的概率;
(2)为进一步提高市民对电动车的使用热情,市政府准备为电动车车主一次性发放补助,标准如下:①电动自行车每辆补助300元;②电动汽车每辆补助500元;③对电池需要更换的电动车每辆额外补助400元.试求抽取的100辆电动车执行此方案的预算;并利用样本估计总体,试估计市政府执行此方案的预算.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() 的最小值为
的最小值为![]() ,
,![]() 的图象的相邻两条对称轴之间的距离为
的图象的相邻两条对称轴之间的距离为![]() ,
,![]() 的图象关于原点对称.
的图象关于原点对称.
(1)求函数![]() 的解析式和单调递增区间;
的解析式和单调递增区间;
(2)在![]() 中,角
中,角![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过
,过![]() 任作一条与两条坐标轴都不垂直的直线,与椭圆
任作一条与两条坐标轴都不垂直的直线,与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() 的周长为8,当直线
的周长为8,当直线![]() 的斜率为
的斜率为![]() 时,
时, ![]() 与
与![]() 轴垂直.
轴垂直.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)在![]() 轴上是否存在定点
轴上是否存在定点![]() ,总能使
,总能使![]() 平分
平分![]() ?说明理由.
?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在平面四边形![]() 中,
中,![]() ,现将
,现将![]() 沿四边形
沿四边形![]() 的对角线
的对角线![]() 折起,使点
折起,使点![]() 运动到点
运动到点![]() ,如图2,这时平面
,如图2,这时平面![]() 平面
平面![]() .
.
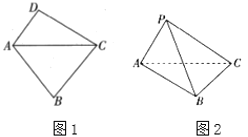
(1)求直线![]() 与平面
与平面![]() 所成角的正切值;
所成角的正切值;
(2)求二面角![]() 的正切值.
的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥![]() 中,
中,![]() 底面
底面![]() 为等边三角形,
为等边三角形,![]() 分别是
分别是![]() 的中点.
的中点.
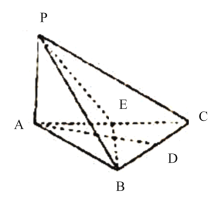
(1)证明:平面![]() 平面
平面![]() ;
;
(2)如何在![]() 上找一点
上找一点![]() ,使
,使![]() 平面
平面![]() 并说明理由;
并说明理由;
(3)若![]() ,对于(2)中的点
,对于(2)中的点![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,已知底面ABCD是矩形,PA⊥平面ABCD,AP=2,AB=2,AD=4,且E、F分别是PB、PC的中点。
中,已知底面ABCD是矩形,PA⊥平面ABCD,AP=2,AB=2,AD=4,且E、F分别是PB、PC的中点。
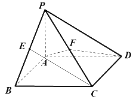
(1)求三棱锥![]() 的体积;
的体积;
(2)求直线EC与平面PCD所成角的大小(结果用反三角函数值表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定数列![]() ,记该数列前
,记该数列前![]() 项
项![]() 中的最大项为
中的最大项为![]() ,即
,即![]() ,该数列后
,该数列后![]() 项
项![]() 中的最小项为
中的最小项为![]() ,记
,记![]() ,
,![]() ;
;
(1)对于数列:3,4,7,1,求出相应的![]() ,
,![]() ,
,![]() ;
;
(2)若![]() 是数列
是数列![]() 的前
的前![]() 项和,且对任意
项和,且对任意![]() ,有
,有![]() ,其中
,其中![]() 为实数,
为实数,![]() 且
且![]() ,
,![]() .
.
(ⅰ)设![]() ,证明:数列
,证明:数列![]() 是等比数列;
是等比数列;
(ⅱ)若数列![]() 对应的
对应的![]() 满足
满足![]() 对任意的正整数
对任意的正整数![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com