Question

　　

（本小题共14分）

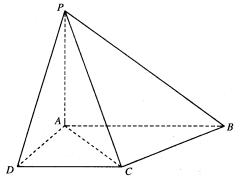
　　四棱锥P—ABCD中，PA⊥底面ABCD，AB//CD，AD=CD=1，∠BAD=120°，PA=，∠ACB=90°。

　　（I）求证：BC⊥平面PAC；

　　（II）求二面角D—PC—A的大小；

　　（III）求点B到平面PCD的距离。

　　

Answer 1

，

解析:

　解法一：

　　证明：（I）∵PA⊥底面ABCD，平面ABCD，

　　∴PA⊥BC

　　∵∠ACB=90°

　　∴BC⊥AC

　　又

　　∴BC⊥平面PAC　　　　　　　　　　　　　　　 4分

　　解：（II）∵AB//CD，∠DAB=120°

　　∴∠ADC=60°，又AD=CD=1

　　∴△ADC为等边三角形，且AC=1　　　　　　 5分

　　取AC的中点O，则DO⊥AC

　　∵PA⊥底面ABCD

　　∴PA⊥DO

　　∴DO⊥平面PAC

　　过O作OH⊥PC，垂足为H，连DH，由三垂线定理知DH⊥PC

　　∴∠DHO为二面角D—PC—A的平面角　　　　　　　　　　　　 7分

　　由　　　　　　　　　　　　　　　　　8分

　　

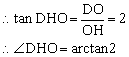
　　∴二面角D—PC—A的大小为arctan2　　　　　　　　　　　　　　9分

　　（III）设点B到平面PCD的距离为d

　　∵AB//CD，平面PCD

　　∴AB//平面PCD

　　∴点B到平面PCD的距离等于点A到平面PCD的距离　　　　　 11分

　　　　　　　　　　　　　　　　　　　　　　　　　 13分

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 14分

　　

　　解法二：

　　证明：（I）同解法一　　　　　　　　　　　　　　　　　　　　　　　 4分

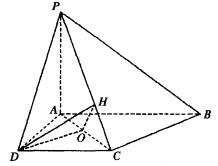
　　解：（II）取CD的中点E，则AE⊥CD

　　∴AE⊥AB

　　又PA⊥底面ABCD，底面ABCD

　　∴PA⊥AE　　　　　　　　　　　　　　　　　　　　　　　　　　 5分

　　建立空间直角坐标系，如图。则

A（0，0，0），

　　

　　　　　　　　　　　　　　　　　　 7分

　　设为平面PAC的一个法向量

　　为平面PDC的一个法向量，则

　　，

　　可取；

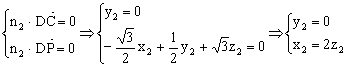　　，可取　 9分

　　　　　　　　　　　　　　　　 10分

　　

　　故所求二面角的大小为　　　　　　　　　　　　　 11分

　　（III）又B（0，2，0），　　　　　　　　　　　　　　 12分

　　由（II）取平面PCD的一个法向量

　　∴点B到平面PCD的距离为

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 13分

　　　　　　　　　　　　　　　　　　　　　　　　　14分