
【题目】试问:能否把2008表示成![]() 的形式?如果可以,这种表示方式是否有无限多个?其中,m、n均为大于100且小于170的正整数,且
的形式?如果可以,这种表示方式是否有无限多个?其中,m、n均为大于100且小于170的正整数,且![]() ;
;![]() 均为两两不相等的小于6的正有理数,且
均为两两不相等的小于6的正有理数,且![]() 均为大于1且小于5的正整数,同时,
均为大于1且小于5的正整数,同时, ![]() 两两不相等,
两两不相等,![]() 也两两不相等请说明理由.
也两两不相等请说明理由.
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.

(1)证明:![]() 平面AEC;
平面AEC;
(2)设AP=1,AD=![]() ,三棱锥P-ABD的体积V=
,三棱锥P-ABD的体积V=![]() ,求A到平面PBC的距离.
,求A到平面PBC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将编号为1,2,…,18的18名乒乓球运动员分配在9张球台上进行单打比赛,规定每一张球台上两选手编号之和均为大于4的平方数.记{7号与18号比赛}为事件p.则p为( ).
A. 不可能事件 B. 概率为![]() 的随机事件
的随机事件
C. 概率为![]() 的随机事件 D. 必然事件
的随机事件 D. 必然事件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间如下:
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |

(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是一个给定的非零实数,在平面直角坐标系
是一个给定的非零实数,在平面直角坐标系![]() 中,曲线
中,曲线![]() 的方程为
的方程为![]() 且
且![]() ,点
,点![]() .
.
(1)设![]() 是
是![]() 上的任意一点,试求线段
上的任意一点,试求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程并指出曲线
的方程并指出曲线![]() 的类型和位置;
的类型和位置;
(2)求出![]() 、
、![]() 在它们的交点
在它们的交点![]() 处的各自切线之间的夹角
处的各自切线之间的夹角![]() (锐角)(用反三角函数式表示)
(锐角)(用反三角函数式表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知钝角△ABC中,∠B-∠C=90°,∠C=θ,其外接圆⊙O的半径为R.AD是⊙O的一条直径,过点D作⊙O的切线与BC的延长线交于H,过点D作BA的平行线交AC的延长线于E,交过D、O、H的圆于G,联结GH、EH.求△EGH的面积.
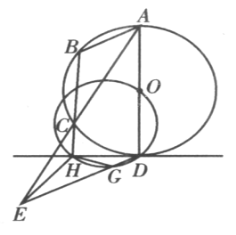
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() 为棱
为棱![]() 上的一点,且
上的一点,且![]() ,
,![]() 为棱
为棱![]() 的中点,
的中点,![]() 为棱
为棱![]() 上的一点,若
上的一点,若![]() 平面
平面![]() ,
,![]() 是边长为4的正三角形,
是边长为4的正三角形,![]() ,
,![]() .
.
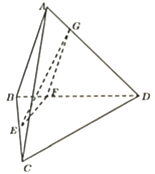
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2021年开始,我省将试行“3+1+2“的普通高考新模式,即除语文、数学、外语3门必选科目外,考生再从物理、历史中选1门,从化学、生物、地理、政治中选2门作为选考科目.为了帮助学生合理选科,某中学将高一每个学生的六门科目综合成绩按比例均缩放成5分制,绘制成雷达图.甲同学的成绩雷达图如图所示,下面叙述一定不正确的是( )

A.甲的物理成绩领先年级平均分最多
B.甲有2个科目的成绩低于年级平均分
C.甲的成绩从高到低的前3个科目依次是地理、化学、历史
D.对甲而言,物理、化学、地理是比较理想的一种选科结果
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,矩形![]() 中,
中,![]() ,
,![]() 是
是![]() 边上异于端点的动点,
边上异于端点的动点,![]() ,将矩形
,将矩形![]() 沿
沿![]() 折叠至
折叠至![]() 处,使面
处,使面![]() (如图2).点
(如图2).点![]() 满足
满足![]() ,
,![]() .
.
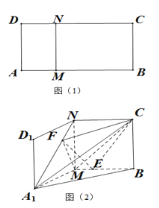
(1)证明:![]() ;
;
(2)设![]() ,当
,当![]() 为何值时,四面体
为何值时,四面体![]() 的体积最大,并求出最大值.
的体积最大,并求出最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com