
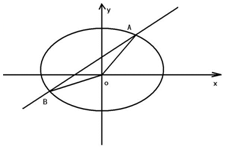
 已知椭圆C的中心在坐标原点,一个焦点的坐标为$(\sqrt{3},0)$,椭圆C经过点P$(1,\frac{{\sqrt{3}}}{2})$.
已知椭圆C的中心在坐标原点,一个焦点的坐标为$(\sqrt{3},0)$,椭圆C经过点P$(1,\frac{{\sqrt{3}}}{2})$.分析 (1)设椭圆方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$.(a>b>0),由题意可得c=$\sqrt{3}$,将P的坐标代入椭圆方程,由a,b,c的关系可得a,b,进而得到椭圆方程;
(2)由|AB|=2,△AOB的面积S=1,可得O到直线AB的距离为2,即b2=1+k2.由弦长公式表示|AB|=2,即可求出直线的斜率k.,b.
解答 解:(1)设椭圆方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$.(a>b>0)∵$\left\{{\begin{array}{l}{c=\sqrt{3}}\\{{a^2}-{b^2}=3}\\{\frac{1}{a^2}+\frac{3}{{4{b^2}}}=1}\end{array}}\right.⇒\left\{{\begin{array}{l}{{a^2}=4}\\{{b^2}=1}\\{{c^2}=3}\end{array}}\right.⇒\begin{array}{l}{∴椭圆的方程为}\\{\frac{x^2}{4}+{y^2}=1}\end{array}$…(4分)
(2)设A(x1,y1),B(x2,y2),O点到AB的距离为d,则由$S=\frac{1}{2}|{AB}|•d=2$,则d=2,
又由距离公式$\frac{|b|}{{\sqrt{1+{k^2}}}}=1$,则b2=1+k2.…①…(6分)
联立$\left\{{\begin{array}{l}{\frac{x^2}{4}+{y^2}=1}\\{y=kx+b}\end{array}}\right.⇒(1+4{k^2}){x^2}+8kbx+4{b^2}-4=0$,即$\left\{{\begin{array}{l}{{x_1}+{x_2}=\frac{-8kb}{{1+4{k^2}}}}\\{{x_1}{x_2}=\frac{{4{b^2}-4}}{{1+4{k^2}}}}\end{array}}\right.$,…(8分)
则$|{AB}|=\sqrt{1+{k^2}}|{{x_1}-{x_2}}|=\sqrt{1+{k^2}}\sqrt{{{(\frac{-8kb}{{1+4{k^2}}})}^2}-4•\frac{{4{b^2}-4}}{{1+4{k^2}}}}$=$\sqrt{1+{k^2}}\sqrt{\frac{{4(16{k^2}+4-4{b^2})}}{{{{(1+4{k^2})}^2}}}}$②
把②代入①,化简可以得到4k4-4k2+1=0,即${k^2}=\frac{1}{2}$,且${b^2}=\frac{3}{2}$,…(11分)
则直线AB的方程为$y=±\frac{{\sqrt{2}}}{2}x±\frac{{\sqrt{6}}}{2}$.…(12分)
点评 本题考查了椭圆的方程的求法,注意运用直线方程和椭圆方程联立,运用韦达定理求弦长,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | -$\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
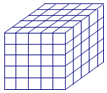 如图,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,记它的涂漆面数为X,则X的均值E(X)=$\frac{6}{5}$.
如图,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,记它的涂漆面数为X,则X的均值E(X)=$\frac{6}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{6}{5}$ | C. | $\frac{36}{5}$ | D. | $\frac{6}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com