
(09年朝阳区二模理)(14分)
如图,四棱锥![]() 的底面是矩形,
的底面是矩形,![]() 底面
底面![]() ,
,![]() 为
为![]() 边的中点,
边的中点,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,且
,且![]() ,
,![]() .
.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求点![]() 到平面
到平面![]() 的距离;
的距离;
(Ⅲ)求二面角![]() 的大小.
的大小.

解析: 证明:(Ⅰ)因为![]() 底面
底面![]() ,
,
所以![]() 是
是![]() 与平面
与平面![]() 所成的角.
所成的角.
由已知![]() , 所以
, 所以![]() .
.
易求得,![]() ,又因为
,又因为![]() ,
,
所以![]() , 所以
, 所以![]() .
.
因为![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() . 由于
. 由于![]() ,
,
所以![]() 平面
平面![]() . ………………………4分
. ………………………4分
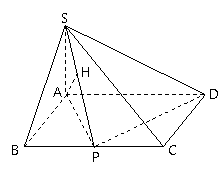
解:(Ⅱ) 由(Ⅰ)知,![]() 平面
平面![]() .又因为
.又因为![]() 平面
平面![]() ,
,
所以平面![]()
![]() 平面
平面![]() ,
,
过![]() 作
作![]()
![]()
![]() 于
于![]() ,(如图)则
,(如图)则![]()
![]() 平面
平面![]() ,
,
所以线段![]() 的长度为点
的长度为点![]() 到平面
到平面![]() 的距离.
的距离.
在![]() 中,易求得
中,易求得![]() , 所以
, 所以![]() .
.
所以点![]() 到平面
到平面![]() 的距离为
的距离为![]() . ………………………9分
. ………………………9分
(Ⅲ)设![]() 为
为![]() 中点. 连结
中点. 连结![]() ,由于
,由于![]() 底面
底面![]() ,
,
且![]() 平面
平面![]() ,则平面
,则平面![]()
![]() 平面
平面![]() .
.
因为![]() ,所以
,所以![]()
![]() 平面
平面![]() .
.
过![]() 作
作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() ,
,
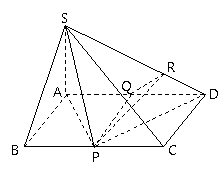
由三垂线定理可知![]() ,
,
所以![]() 是二面角
是二面角![]() 的平面角.
的平面角.
容易证明![]() ∽
∽![]() ,则
,则![]() ,
,
因为![]() ,
,![]() ,
,![]() ,
,
所以![]() .
.
在![]() 中,因为
中,因为![]() ,所以
,所以![]() ,
,
所以二面角![]() 的大小为
的大小为![]() . ………………………14分
. ………………………14分
解法二:
因为![]() 底面
底面![]() ,
,
所以![]() 是
是![]() 与平面
与平面![]() 所成的角.
所成的角.
由已知![]() ,
,
所以![]() .
.
建立空间直角坐标系(如图).
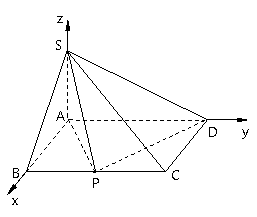
由已知,![]() 为
为![]() 中点.
中点.
于是![]() 、
、![]() 、
、![]() 、
、
![]() 、
、![]() .
.
(Ⅰ)易求得![]() ,
,
![]() ,
, ![]() .
.
因为![]() ,
, ![]() ,
,
所以![]() ,
,![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() . ………………………4分
. ………………………4分
(Ⅱ)设平面![]() 的法向量为
的法向量为![]() ,
,
由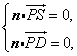 得
得![]() 解得
解得![]() ,
,
所以![]() . 又因为
. 又因为![]() ,
,
所以点![]() 到平面
到平面![]() 的距离
的距离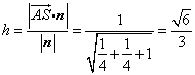 . …………………9分
. …………………9分
(Ⅲ)因为![]() 平面
平面![]() ,所以
,所以![]() 是平面
是平面![]() 的法向量, 易得
的法向量, 易得![]() .
.
由(Ⅱ)知平面![]() 的法向量
的法向量![]() ,
,
所以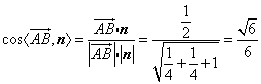 .
.
所以二面角![]() 的大小为
的大小为![]() . ………………………14分
. ………………………14分


科目:高中数学 来源: 题型:
(09年朝阳区二模理)(14分)
已知函数![]() .
.
(Ⅰ)求函数![]() 的最小值;
的最小值;
(Ⅱ)求证:![]()
![]() ;
;
(Ⅲ)对于函数![]() 与
与![]() 定义域上的任意实数
定义域上的任意实数![]() ,若存在常数
,若存在常数![]() ,使得
,使得![]() 和
和![]() 都成立,则称直线
都成立,则称直线![]() 为函数
为函数![]() 与
与![]() 的“分界线”.设函数
的“分界线”.设函数![]() ,
,![]() ,
,![]() 与
与![]() 是否存在“分界线”?若存在,求出
是否存在“分界线”?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年朝阳区二模理)(13分)
在袋子中装有10个大小相同的小球,其中黑球有3个,白球有![]() ,且
,且![]() 个,其余的球为红球.
个,其余的球为红球.
(Ⅰ)若![]() ,从袋中任取1个球,记下颜色后放回,连续取三次,求三次取出的球中恰有2个红球的概率;
,从袋中任取1个球,记下颜色后放回,连续取三次,求三次取出的球中恰有2个红球的概率;
(Ⅱ)从袋里任意取出2个球,如果这两个球的颜色相同的概率是![]() ,求红球的个数;
,求红球的个数;
(Ⅲ)在(Ⅱ)的条件下,从袋里任意取出2个球.若取出1个白球记1分,取出1个黑球记2分,取出1个红球记3分.用ξ表示取出的2个球所得分数的和,写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com