已函数
是定义在
上的奇函数,在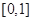
上时
（Ⅰ）求函数的解析式;
（Ⅱ）解不等式
．
（Ⅰ）
;（Ⅱ）[0,1]
解析试题分析：（Ⅰ）由奇函数及在[0,1]上的解析式可得函数在[-1,0]上的解析式.从而即可得在[-1,1]上的解析式.本小题主要是考查分段函数的解析式问题.
（Ⅱ）由题意可知函数f(x)在[-1,1]上是递增函数.又因为函数f(x)是奇函数.所以通过可得.
所以可得
.从而可解得结论.本小题关键是通过函数的单调递增把函数值的大小转化为自变量的大小比较.
试题解析：（Ⅰ）设
.则
.所以
.又f(x)是奇函数.所以f(-x)="-f(x).f(x)=-f(-x)=" 
.所以
.
（Ⅱ）易知f(x)是[-1,1]上增函数.由已知得.等价于
.所以不等式的解集为[0,1].
考点：1.分段函数.2.函数的单调性.3.函数的奇偶性.
科目：高中数学 来源： 题型：解答题
定义在
上的函数
，如果对任意
，恒有
（
，
）成立，则称为
阶缩放函数.
（1）已知函数为二阶缩放函数，且当
时，
，求
的值；
（2）已知函数为二阶缩放函数，且当时，
，求证：函数
在
上无零点；
（3）已知函数为阶缩放函数，且当
时，的取值范围是
，求在
（
）上的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
定义在
上的函数
满足：①对任意
都有：
；②当
时，
，回答下列问题．
（1）证明：函数在上的图像关于原点对称；
（2）判断函数在
上的单调性，并说明理由．
（3）证明：
，
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
,函数
.
在
上单调递增；
的图象经过点
．
上的单调性，并用单调性的定义证明．
的定义域为R，求实数m的取值范围.
在
上是减函数，且为奇函数，满足
，试
求的范围．
在
上单调递增；
的值；
，求
，求它的定义域和值域。