
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi , yi)(i=1,2,…,n),用最小二乘法建立的回归方程为 ![]() =0.85x﹣85.71,则下列结论中不正确的是( )
=0.85x﹣85.71,则下列结论中不正确的是( )
A.y与x具有正的线性相关关系
B.回归直线过样本点的中心( ![]() ,
, ![]() )
)
C.若该大学某女生身高增加1cm,则其体重约增加0.85kg
D.若该大学某女生身高为170cm,则可断定其体重必为58.79kg
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB= ![]() =AC=2,E,F分别为A1C1 , BC的中点.
=AC=2,E,F分别为A1C1 , BC的中点. 
(1)求证:平面ABE⊥平面B1BCC1;
(2)求证:C1F∥平面ABE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+2|﹣|x+a|
(1)当a=3时,解不等式f(x)≤ ![]() ;
;
(2)若关于x的不等式f(x)≤a解集为R,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=![]() ,AC=3, BC=2,P是△ABC内的一点.
,AC=3, BC=2,P是△ABC内的一点.
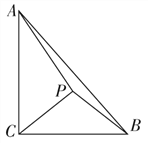
(1)若P是等腰直角三角形PBC的直角顶点,求PA的长;
(2)若∠BPC=![]() ,设∠PCB=θ,求△PBC的面积S(θ)的解析式,并求S(θ)的最大值.
,设∠PCB=θ,求△PBC的面积S(θ)的解析式,并求S(θ)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某著名歌星在某地举办一次歌友会,有1000人参加,每人一张门票,每张100元.在演出过程中穿插抽奖活动,第一轮抽奖从这1000张票根中随机抽取10张,其持有者获得价值1000元的奖品,并参加第二轮抽奖活动.第二轮抽奖由第一轮获奖者独立操作按钮,电脑随机产生两个实数x,y(x,y∈[0,4]),若满足y≥ ![]() ,电脑显示“中奖”,则抽奖者再次获得特等奖奖金;否则电脑显示“谢谢”,则不获得特等奖奖金.
,电脑显示“中奖”,则抽奖者再次获得特等奖奖金;否则电脑显示“谢谢”,则不获得特等奖奖金.
(1)已知小明在第一轮抽奖中被抽中,求小明在第二轮抽奖中获奖的概率;
(2)设特等奖奖金为a元,小李是此次活动的顾客,求小李参加此次活动获益的期望;若该歌友会组织者在此次活动中获益的期望值是至少获得70000元,求a的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为获得较好的收益,每年要投入一定资金用于广告促销,经调查,每年投入广告费![]() (百万元),可增加销售额约为
(百万元),可增加销售额约为![]() (百万元)(
(百万元)(![]() )
)
(1)若该公司当年的广告费控制在4百万元之内,则应该设入多少广告费,才能使该公司获得的收益最大?
(2)现该公司准备共投入6百万元,分别用于广告促销售和技术改造,经预测,每设入技术改造费![]() (百万元),可增加销售额约为
(百万元),可增加销售额约为![]() (百万元),请设计一种资金分配方案,使该公司由此获得最大收益.(注:收益
(百万元),请设计一种资金分配方案,使该公司由此获得最大收益.(注:收益![]() 销售额
销售额![]() 成本)
成本)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com