
【题目】设![]() .
.
(1)证明: ![]() 在
在![]() 上单调递减;
上单调递减;
(2)若![]() ,证明:
,证明: ![]() .
.
【答案】(1)见解析;(2)见解析
【解析】试题分析:(1)第(1)问,直接求导,证明0<x<1时, f(x)<0 .(2)第(2)问,
分0<a≤![]() 和
和![]() <a<1两种情况证明,每一种情况都是先通过求单调性再求函数的最小值大于1.
<a<1两种情况证明,每一种情况都是先通过求单调性再求函数的最小值大于1.
试题解析:
(1)f(x)=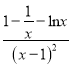 .
.
令h(x)=1-![]() -lnx,则h(x)=
-lnx,则h(x)=![]() ,x>0,
,x>0,
所以0<x<1时,h(x)>0,h(x)单调递增,
又h(1)=0,所以h(x)<0,
即f(x)<0,所以f(x)单调递减.
(2)g(x)=axlna+axa-1=a(ax-1lna+xa-1),
当0<a≤![]() 时,lna≤-1,所以ax-1lna+xa-1≤xa-1-ax-1.
时,lna≤-1,所以ax-1lna+xa-1≤xa-1-ax-1.
由(Ⅰ)得![]() ,所以(a-1)lnx<(x-1)lna,即xa-1<ax-1,
,所以(a-1)lnx<(x-1)lna,即xa-1<ax-1,
所以g(x)<0,g(x)在(a,1)上单调递减,
即g(x)>g(1)=a+1>1.
当![]() <a<1时,-1<lna<0.
<a<1时,-1<lna<0.
令t(x)=ax-xlna-1,0<a<x<1,则t(x)=axlna-lna=(ax-1)lna>0,
所以t(x)在(0,1)上单调递增,即t(x)>t(0)=0,
所以ax>xlna+1
所以g(x)=ax+xa>xa+xlna+1=x(xa-1+lna)+1>x(1+lna)+1>1.
综上,g(x)>1.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:
【题目】在多面体![]() 中,四边形
中,四边形![]() 是正方形,平面
是正方形,平面![]() 平面
平面![]() ,
,![]() .
.
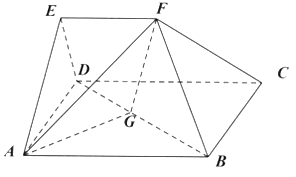
(1)求证:![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成的锐二面角的大小为
所成的锐二面角的大小为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 上一点
上一点![]() 到左右两个焦点
到左右两个焦点![]() 的距离之和是4.
的距离之和是4.
(1)求椭圆的方程;
(2)已知过![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,且两点与左右顶点不重合,若
两点,且两点与左右顶点不重合,若![]() ,求四边形
,求四边形![]() 面积的最大值。
面积的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别是所在棱
分别是所在棱![]() 、
、![]() 的中点,点
的中点,点![]() 是棱
是棱![]() 上的动点,联结
上的动点,联结![]() ,
,![]() .如图所示.
.如图所示.
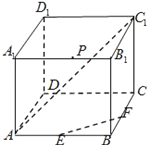
(1)求异面直线![]() ,
,![]() 所成角的大小(用反三角函数值表示);
所成角的大小(用反三角函数值表示);
(2)(理科)求以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的三棱锥的体积.
为顶点的三棱锥的体积.
(文科)求以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的三棱锥的体积.
为顶点的三棱锥的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,在五边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是以
是以![]() 为斜边的等腰直角三角形.现将
为斜边的等腰直角三角形.现将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,如图②,记线段
,如图②,记线段![]() 的中点为
的中点为![]() .
.
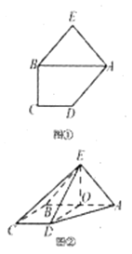
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成的锐二面角的大小.
所成的锐二面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中的真命题是( )
A. 若![]() ,则向量
,则向量![]() 与
与![]() 的夹角为钝角
的夹角为钝角
B. 若![]() ,则
,则![]()
C. 若命题“![]() 是真命题”,则命题“
是真命题”,则命题“![]() 是真命题”
是真命题”
D. 命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】河道上有一抛物线型拱桥,在正常水位时,拱圈最高点距水面8m,拱圈内水面宽24m,一条船在水面以上部分高6.5m,船顶部宽6m.
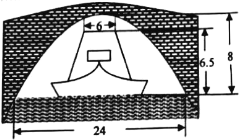
(1)试建立适当的直角坐标系,求拱桥所在的抛物线的标准方程;
(2)近日水位暴涨了1.54m,为此,必须加重船载,降低船身,才能通过桥洞,试问:船身至少应该降低多少?(精确到0.1m)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设抛物线![]() 与
与![]() 的公共点
的公共点![]() 的横坐标为
的横坐标为![]() ,过
,过![]() 且与
且与![]() 相切的直线交
相切的直线交![]() 于另一点
于另一点![]() ,过
,过![]() 且与
且与![]() 相切的直线交
相切的直线交![]() 于另一点
于另一点![]() ,记
,记![]() 为
为![]() 的面积.
的面积.
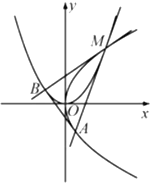
(Ⅰ)求![]() 的值(用
的值(用![]() 表示);
表示);
(Ⅱ)若![]() ,求
,求![]() 的取值范围.
的取值范围.
注:若直线与抛物线有且只有一个公共点,且与抛物线的对称轴不平行也不重合,则称该直线与抛物线相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着互联网经济不断发展,网上开店销售农产品的人群越来越多,网上交易额也逐年增加,某一农户农产品连续五年的网银交易额统计表,如下所示:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
网上交易额 | 5 | 6 | 7 | 8 | 10 |
经研究发现,年份与网银交易额之间呈线性相关关系,为了计算的方便,农户将上表的数据进行了处理,![]() ,得到如表:
,得到如表:
时间代号 | 1 | 2 | 3 | 4 | 5 |
| 0 | 1 | 2 | 3 | 5 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)通过(1)中的方程.求出![]() 关于
关于![]() 的回归方程;并用所求回归方程预测到2020年年底,该农户网店网银交易额可达多少?
的回归方程;并用所求回归方程预测到2020年年底,该农户网店网银交易额可达多少?
(附:在线性回归方程![]() 中,
中,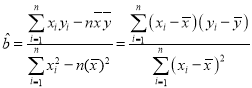 ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com