练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数（， ）.

    （1）当时，讨论函数的单调区间；

    （2）当时，若对任意恒成立，求的取值范围.

    【答案】（1）见解析；（2）.

    【解析】试题分析：（1）求导数，由导数大于0求增区间，导数小于0求减区间；

    （2）讨论和三种情况，研究函数的单调性和最值即可.
    试题解析：

    （1）当时， ， ，

    ①当时， ，所以函数的单调递增区间为；

    ②当时，可知： ，所以当时， ；

    当时， ；

    所以函数的单调递增区间为，递减区间为.

    （2）当时， ， ，

    若，此时对任意都有， ，

    所以恒成立；

    下面考虑时的情况：

    若，对任意都有， ，所以，所以为上的增函数，所以，即时满足题意；

    若，则由， ，可知：一定存在，使得，且当时， ，所以在上， 单调递减，从而有： 时，不满足题意.

    综上可知， 的取值范围为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】学校为了解学生在课外读物方面的支出情况，抽取了n名同学进行调查，结果显示这些同学的支出都在[10,50)(单位：元)，其中支出在[30,50)(单位：元)的同学有67人，其频率分布直方图如图所示，则n的值为(　　)

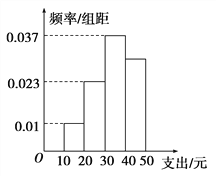
    A. 100 B. 120 C. 130 D. 390

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题10分） 从3名男生和名女生中任选2人参加比赛。

    ①求所选2人都是男生的概率;

    ②求所选2人恰有1名女生的概率;

    ③求所选2人中至少有1名女生的概率

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】近期中央电视台播出的《中国诗词大会》火遍全国，下面是组委会在选拔赛时随机抽取的100名选手的成绩，按成绩分组，得到的频率分布表如下所示：

    组号

    分组

    频数

    频率

    第1组

    第2组

    ①

    第3组

    20

    ②

    第4组

    20

    第5组

    10

    合计

    100

    （1）请先求出频率分布表中①、②位置的相应数据，再完成频率分布直方图（用阴影表示）；

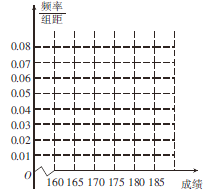
    （2）为了能选拔出最优秀的选手，组委会决定在笔试成绩高的第3、4、5组中用分层抽样抽取5名选手进入第二轮面试，求第3、4、5组每组各抽取多少名选手进入第二轮面试；

    （3）在（2）的前提下，组委会决定在5名选手中随机抽取2名选手接受考官进行面试，求：第4组至少有一名选手被考官面试的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，内角A，B，C对边的边长分别是a，b，c，已知c=2，C= ．
    （1）若△ABC的面积等于 ，求a，b；
    （2）若sinC+sin（B﹣A）=2sin2A，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=Asin（x+φ）（A＞0，0＜φ＜π），x∈R的最大值是1，其图象经过点 ．
    （1）求f（x）的解析式；
    （2）已知 ，且 ， ，求f（α﹣β）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，已知定点A(－4，0)、C(4，0)，半径为r的圆M的圆心M在线段AC的垂直平分线上，且在y轴右侧，圆M被y轴截得的弦长为 r.

    (1)求圆M的方程；（2)当r变化时，是否存在定直线l与动圆M均相切？如果存在，求出定直线l的方程；如果不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义平面向量之间的一种运算“⊙”如下：对任意的 ，令 ⊙ =mq-np，下面说法错误的是（ ）
    A.若 与 共线，则 ⊙ =0
    B. ⊙ = ⊙
    C.对任意的λ∈R，有 ⊙ = ⊙ ）
    D.（ ⊙ ）2+（ ）2=| |2| |2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

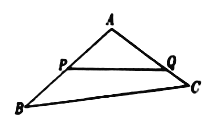
    【题目】如图，某生态园将一块三角形地的一角开辟为水果园，已知角为， 的长度均大于200米，现在边界处建围墙，在处围竹篱笆.

    （1）若围墙、总长度为200米，如何可使得三角形地块面积最大？

    （2）已知竹篱笆长为米， 段围墙高1米， 段围墙高2米，造价均为每平方米100元，若，求围墙总造价的取值范围.

    查看答案和解析>>

    同步练习册答案