
【题目】数列{an}满足a1= ![]() ,an+1=an2﹣an+1(n∈N*),则m=
,an+1=an2﹣an+1(n∈N*),则m= ![]() +
+ ![]() +…+
+…+ ![]() 的整数部分是( )
的整数部分是( )
A.0
B.1
C.2
D.3
科目:高中数学 来源: 题型:
【题目】在△ABC中,A,B,C的对边分别是a,b,c,3sin2C+8sin2A=11sinAsinC,且c<2a.
(1)求证:△ABC为等腰三角形
(2)若△ABC的面积为8 ![]() .且sinB=
.且sinB= ![]() ,求BC边上的中线长.
,求BC边上的中线长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位为了了解用电量y度与气温x℃之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
气温/℃ | 18 | 13 | 10 | -1 |
用电量/度 | 24 | 34 | 38 | 64 |
由表中数据得线性回归方程![]() 中,
中,![]() ≈-2,预测当气温为-4℃时,用电量为多少.
≈-2,预测当气温为-4℃时,用电量为多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四种说法中,
①命题“存在x∈R,x2﹣x>0”的否定是“对于任意x∈R,x2﹣x<0”;
②命题“p且q为真”是“p或q为真”的必要不充分条件;
③已知幂函数f(x)=xα的图象经过点(2, ![]() ),则f(4)的值等于
),则f(4)的值等于 ![]() ;
;
④已知向量 ![]() =(3,﹣4),
=(3,﹣4), ![]() =(2,1),则向量
=(2,1),则向量 ![]() 在向量
在向量 ![]() 方向上的投影是
方向上的投影是 ![]() .
.
说法错误的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得![]() =80,
=80, ![]() =20,
=20, ![]() =184,
=184, ![]() =720.
=720.
(1)求家庭的月储蓄y对月收入x的线性回归方程y=bx+a;
(2)判断变量x与y之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:线性回归方程y=bx+a中,  ,a=
,a=![]() -b
-b![]() ,其中
,其中![]() ,
, ![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣a|+|x﹣1|.
(1)当a=3时,求不等式f(x)≥2的解集;
(2)若f(x)≥5﹣x对x∈R恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
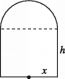
【题目】某制瓶厂要制造一批轴截面如图所示的瓶子,瓶子是按照统一规格设计的,瓶体上部为半球体,下部为圆柱体,并保持圆柱体的容积为3π.设圆柱体的底面半径为x,圆柱体的高为h,瓶体的表面积为S.
(1)写出S关于x的函数关系式;
(2)如何设计瓶子的尺寸(不考虑瓶壁的厚度),可以使表面积S最小,并求出最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com