
【题目】已知集合A={x|x2-6x+8<0}, ![]() .
.
(1)若x∈A是x∈B的充分条件,求a的取值范围.
(2)若A∩B=,求a的取值范围.
【答案】
(1)解:当a=0时,B=,不合题意.
当a>0时,B={x|a<x<3a},要满足题意,
则 ![]() 解得
解得 ![]() ≤a≤2.
≤a≤2.
当a<0时,B={x|3a<x<a},要满足题意,
则 ![]() 无解.
无解.
综上,a的取值范围为 ![]() .
.
(2)解:要满足A∩B=,
当a>0时,B={x|a<x<3a}则a≥4或3a≤2,即0<a≤ ![]() 或a≥4.
或a≥4.
当a<0时,B={x|3a<x<a},则a≤2或a≥ ![]() ,即a<0.
,即a<0.
当a=0时,B=,A∩B=.
综上,a的取值范围为 ![]() ∪[4,+∞)
∪[4,+∞)
【解析】(1)对a分情况讨论解出集合B,再结合x∈A是x∈B的充分条件得到关于边界点的范围分别求出a的取值范围并起来即可。(2)利用已知条件A∩B=,对a分情况讨论求出集合B讨论边界点的范围进而得到a的范围并起三种情况下的a的取值范围即可。


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售价格x(单位:元/千克)满足关系式:y= ![]() +10(x﹣6)2 , 其中3<x<6,a为常数,已知销售的价格为5元/千克时,每日可以售出该商品11千克.
+10(x﹣6)2 , 其中3<x<6,a为常数,已知销售的价格为5元/千克时,每日可以售出该商品11千克.
(1)求a的值;
(2)若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形![]() 是正方形,
是正方形, ![]() 平面
平面![]() ,
, ![]() 分别为
分别为![]() 的中点,且
的中点,且![]() .
.
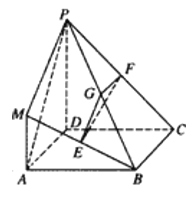
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 与四棱锥
与四棱锥![]() 的体积之比.
的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等比数列,a1=2,且a1 , a3+1,a4成等差数列.
(1)求数列{an}的通项公式;
(2)若bn=log2an , 求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系 ![]() 中,以原点O为极点,x轴的非负半轴为极轴建立极坐标系,直线
中,以原点O为极点,x轴的非负半轴为极轴建立极坐标系,直线 ![]() 的极坐标方程是
的极坐标方程是 ![]() ,圆
,圆 ![]() 的极坐标方程是
的极坐标方程是 ![]() .
.
(1)求 ![]() 与
与 ![]() 交点的极坐标;
交点的极坐标;
(2)设 ![]() 为
为 ![]() 的圆心,
的圆心, ![]() 为
为 ![]() 与
与 ![]() 交点连线的中点,已知直线
交点连线的中点,已知直线 ![]() 的参数方程是
的参数方程是  (
( ![]() 为参数),求
为参数),求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市出租车的收费标准是:3千米以内(含3千米),收起步价8元;3千米以上至8千米以内(含8千米),超出3千米的部分按![]() 元/千米收取;8千米以上,超出8千米的部分按2元/千米收取.
元/千米收取;8千米以上,超出8千米的部分按2元/千米收取.
(1)计算某乘客搭乘出租车行驶7千米时应付的车费;
(2)试写出车费![]() (元)与里程
(元)与里程![]() (千米)之间的函数解析式并画出图像;
(千米)之间的函数解析式并画出图像;

(3)小陈周末外出,行程为10千米,他设计了两种方案:
方案1:分两段乘车,先乘一辆行驶5千米,下车换乘另一辆车再行5千米至目的地
方案2:只乘一辆车至目的地,试问:以上哪种方案更省钱,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com