
分析 根据条件作出函数f(x)的图象,利用换元法转化为t=f(x)的方程根的个数问题,利用数形结合进行求解即可.
解答 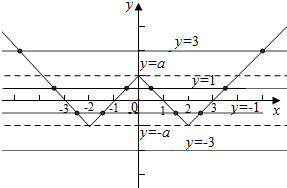 解:由已知可得:当a>0时,f(x)=a|x-2|-a=a(|x-2|-1)的图象如下图所示:
解:由已知可得:当a>0时,f(x)=a|x-2|-a=a(|x-2|-1)的图象如下图所示:
若f(x)=0,则(|x-2|-1=0,即|x-2|=1,则x=1或x=3,
∵函数f(x)是偶函数,∴x=-1,或x=-3也是函数的零点,
即函数f(x)的零点为x=±1,或x=±3,
设t=f(x),
则当t>a时,方程f(x)=t有2个交点,
当t=a时,方程f(x)=t有3个交点,
当-a<t<a时,方程f(x)=t有4个交点,
当t=-a时,方程f(x)=t有2个交点,
当t<-a时,方程f(x)=t有0个交点,
由y=f[f(x)]=0,得f(t)=0,
则t=±1,或t=±3,
若y=f[f(x)]有10个零点,则等价为f(x)=t分别有4,4,2,0个交点,
由对称性可知当t=1或t=-1时,各有4个交点,当t=3时有2个交点,当t=-3有0个交点,
即1<a<3,
故实数a的取值范围为:(1,3),
故答案为:(1,3)
点评 本题考查的知识点是函数的奇偶性,函数的零点,分类讨论思想,数形结合思想,综合性强,分类复杂,属于难题.


科目:高中数学 来源: 题型:解答题
| 性别 是否公平 | 男 | 女 |
| 公平 | 40 | 30 |
| 不公平 | 160 | 270 |
| P(K2≥k) | 0.000 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,侧面ACC1A1⊥侧面BB1C1C,AC⊥CC1.
如图,在三棱柱ABC-A1B1C1中,侧面ACC1A1⊥侧面BB1C1C,AC⊥CC1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
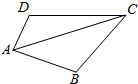 如图所示,已知四边形ABCD各边的长分别为AB=5,BC=5,CD=8,DA=3,且点A、B、C、D在同一个圆上,则对角线AC的长为$\frac{55}{7}$.
如图所示,已知四边形ABCD各边的长分别为AB=5,BC=5,CD=8,DA=3,且点A、B、C、D在同一个圆上,则对角线AC的长为$\frac{55}{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com