
分析 对a讨论,分当0<a≤1时,当1<a≤e时,当a>e时,去掉绝对值,求得导数,判断单调性,即可得到所求最小值.
解答 解:①当0<a≤1时,函数g(x)=|x-a|+$\frac{lnx}{x}$=x-a+$\frac{lnx}{x}$,x∈[1,e],
导数为g′(x)=1+$\frac{1-lnx}{{x}^{2}}$,由x∈[1,e],可得lnx∈[0,1],x2∈[1,e2],
即有g′(x)>0,g(x)递增,可得g(x)min=g(1)=1-a;
②当1<a≤e时,当x≥a时,g(x)=x-a+$\frac{lnx}{x}$,x∈[1,e],
导数为g′(x)=1+$\frac{1-lnx}{{x}^{2}}$,可得g(x)在(a,e)递增;
当x<a时,g(x)=a-x+$\frac{lnx}{x}$,x∈[1,e],
导数为g′(x)=-1+$\frac{1-lnx}{{x}^{2}}$,可得g(x)在(1,a)递减.
即有g(x)在x=a处取得最小值g(a)=$\frac{lna}{a}$;
③当a>e时,g(x)=a-x+$\frac{lnx}{x}$,x∈[1,e],
导数为g′(x)=-1+$\frac{1-lnx}{{x}^{2}}$,可得g(x)在[1,e]递减.
即有g(x)在x=e处取得最小值g(e)=a-e+$\frac{1}{e}$.
综上可得,g(x)min=$\left\{\begin{array}{l}{1-a,0<a≤1}\\{\frac{lna}{a},1<a≤e}\\{a-e+\frac{1}{e},a>e}\end{array}\right.$.
故答案为:$\left\{\begin{array}{l}{1-a,0<a≤1}\\{\frac{lna}{a},1<a≤e}\\{a-e+\frac{1}{e},a>e}\end{array}\right.$.
点评 本题考查函数的最值的求法,注意运用分类讨论的思想方法,以及绝对值的意义和导数的运用:求单调区间和最值,考查化简整理的运算能力,属于中档题.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 大前提错导致结论错 | B. | 小前提错导致结论错 | ||
| C. | 推理形式错导致结论错 | D. | 大前提和小前提错导致结论错 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
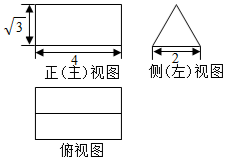 已知一个三棱柱的底面是正三角形,且侧棱垂直于底面,此三棱柱的三视图如图所示,则该棱柱的全面积为( )
已知一个三棱柱的底面是正三角形,且侧棱垂直于底面,此三棱柱的三视图如图所示,则该棱柱的全面积为( )| A. | 24+$\sqrt{3}$ | B. | 24+2$\sqrt{3}$ | C. | 14$\sqrt{3}$ | D. | 12$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,+∞) | B. | (-2,-1) | C. | (-1,1) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com