
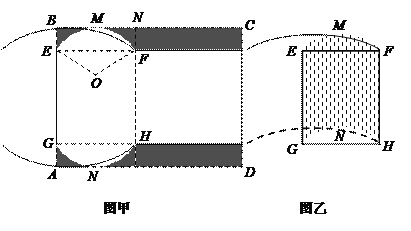
【题目】有一矩形硬纸板材料(厚度忽略不计),一边![]() 长为6分米,另一边足够长.现从中截取矩形
长为6分米,另一边足够长.现从中截取矩形![]() (如图甲所示),再剪去图中阴影部分,用剩下的部分恰好能折卷成一个底面是弓形的柱体包装盒(如图乙所示,重叠部分忽略不计),其中
(如图甲所示),再剪去图中阴影部分,用剩下的部分恰好能折卷成一个底面是弓形的柱体包装盒(如图乙所示,重叠部分忽略不计),其中![]() 是以
是以![]() 为圆心、
为圆心、![]() 的扇形,且弧
的扇形,且弧![]() ,
,![]() 分别与边
分别与边![]() ,
, ![]() 相切于点
相切于点![]() ,
, ![]() .
.
(1)当![]() 长为1分米时,求折卷成的包装盒的容积;
长为1分米时,求折卷成的包装盒的容积;
(2)当![]() 的长是多少分米时,折卷成的包装盒的容积最大?
的长是多少分米时,折卷成的包装盒的容积最大?
【答案】(1)当![]() 长为1分米时,折卷成的包装盒的容积为
长为1分米时,折卷成的包装盒的容积为![]() 立方分米.(2)当
立方分米.(2)当![]() 的长为2分米时,折卷成的包装盒的容积最大
的长为2分米时,折卷成的包装盒的容积最大
【解析】试题分析:(1)先根据扇形面积减去三角形面积得弓形面积,即为柱体底面积,再根据柱体体积公式求体积(2)同(1)先计算底面积,再表示高,代入柱体体积公式得容积函数关系式,最后利用导数求最值
试题解析:解:(1)在图甲中,连接![]() 交
交![]() 于点
于点![]() .设
.设![]() ,
,
在![]() 中,因为
中,因为![]() ,所以
,所以![]() ,则
,则![]() .
.
从而![]() ,即
,即![]() .
.
故所得柱体的底面积![]()
![]() .
.
又所得柱体的高![]() ,
,
所以![]()
![]() .
.
答:当![]() 长为1分米时,折卷成的包装盒的容积为
长为1分米时,折卷成的包装盒的容积为![]() 立方分米.
立方分米.
(2)设![]() ,则
,则![]() ,所以所得柱体的底面积
,所以所得柱体的底面积
![]()
![]() .
.
又所得柱体的高![]() ,
,
所以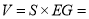
![]() ,其中
,其中![]() .
.
令![]() ,则由
,则由![]() ,
,
解得![]() .
.
列表如下:
|
|
|
|
| + | 0 | - |
| 增 | 极大值 | 减 |
所以当![]() 时,
时, ![]() 取得最大值.
取得最大值.
答:当![]() 的长为2分米时,折卷成的包装盒的容积最大.
的长为2分米时,折卷成的包装盒的容积最大.


科目:高中数学 来源: 题型:
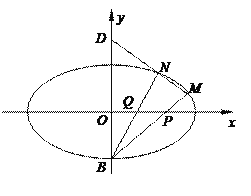
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的下顶点为
的下顶点为![]() ,点
,点![]() 是椭圆上异于点
是椭圆上异于点![]() 的动点,直线
的动点,直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,且点
,且点![]() 是线段
是线段![]() 的中点.当点
的中点.当点![]() 运动到点
运动到点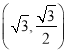 处时,点
处时,点![]() 的坐标为
的坐标为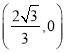 .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 交
交![]() 轴于点
轴于点![]() ,当点
,当点![]() 均在
均在![]() 轴右侧,且
轴右侧,且![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示为一正方体的平面展开图,在这个正方体中,有下列四个命题:
①AF⊥GC;
②BD与GC成异面直线且夹角为60;
③BD∥MN;
④BG与平面ABCD所成的角为45.
其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设S是实数集R的非空子集,若对任意x,y∈S,都有x+y,x-y,xy∈S,则称S为封闭集.下列命题:①集合S={a+b![]() |a,b为整数}为封闭集;②若S为封闭集,则一定有0∈S;③封闭集一定是无限集;④若S为封闭集,则满足STR的任意集合T也是封闭集.其中真命题是________.(写出所有真命题的序号)
|a,b为整数}为封闭集;②若S为封闭集,则一定有0∈S;③封闭集一定是无限集;④若S为封闭集,则满足STR的任意集合T也是封闭集.其中真命题是________.(写出所有真命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com