【题目】设关于
的一元二次方程. 
.
(1)若
是从0、1、2、3四个数中任取的一个数， 
是从0、1、2三个数中任取的一个数，求上述方程有实数根的概率；
(2)若
是从区间
任取的一个数， 
是从区间
任取的一个数，求上述方程有实数根的概率.
【答案】(1) 
(2) 
【解析】试题分析：（1）由一元二次方程的判别式大于等于0得到方程
有实数根的充要条件为a≥b，用列举法求出a从0，1，2，3四个数中任取的一个数，b从0，1，2三个数中任取的一个数的所有基本事件个数，查出满足a≥b的事件数，然后直接利用古典概型的概率计算公式求解；（2）由题意求出点（a，b）所构成的矩形面积，再由线性规划知识求出满足a≥b的区域面积，由测度比是面积比求概率.
试题解析：
设事件
为“方程
有实根”，
方程
有实根的充要条件为
.
(1)基本事件共 12 个：
，
其中括号第一个数表示
的取值袁第二个数表示
的取值.
事件
中包含 9 个基本事件， 
，事件
发生的概率为； 
；
(2)试验的全部结束所构成的区域为
，
构成事件
的区域为
，
所以所求的概率为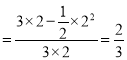
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】已知在四棱锥P﹣ABCD中，底面ABCD是矩形，且AD=2，AB=1，PA⊥平面ABCD，E，F分别是线段AB，BC的中点．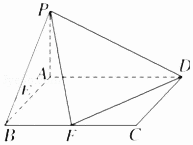 
（1）证明：PF⊥FD；
（2）若PA=1，求点E到平面PFD的距离．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
有如下性质：如果常数
，那么该函数
上是减函数，在
上是增函数．
（1）用函数单调性定义来证明
上的单调性；
（2）已知
， 
，求函数
的值域；
（3）对于（2）中的函数
和函数
，若对任意
，总存在
，使得
成立，求实数
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】定义在R上的奇函数f（x）满足f（x﹣2）=f（x+2），且当x∈[﹣2，0]时，f（x）=3x﹣1，则f（9）=（ ）
A.﹣2
B.2
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在三棱柱
与四棱锥
的组合体中，已知
平面
，四边形
是平行四边形， 
， 
， 
， 
，设
是线段
中点.
(1)求证： 
平面
；
(2)证明：平面
平面
；
(3)求四棱锥
的体积.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知f（x）＝－3x2＋a（6－a）x＋6.
（1）解关于a的不等式f（1）>0；
（2）若不等式f（x）>b的解集为（－1,3），求实数a，b的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
