
 的图象过原点,且关于点(-1,1)成中心对称.
的图象过原点,且关于点(-1,1)成中心对称.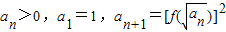 ,求数列an的通项公式an.
,求数列an的通项公式an.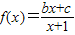 的图象过原点,即f(0)=0,可以解出c=0,再有对称性可以求出b值,即得函数的解析式.
的图象过原点,即f(0)=0,可以解出c=0,再有对称性可以求出b值,即得函数的解析式.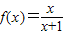 ,故可得
,故可得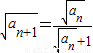 ,即
,即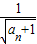 =
=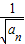 +1,所以
+1,所以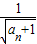 -
-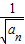 =1由此可以得到 数列{
=1由此可以得到 数列{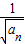 }的性质的,可求数列an的通项公式.
}的性质的,可求数列an的通项公式.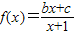 的图象过原点,即f(0)=0,所以c=0,即
的图象过原点,即f(0)=0,所以c=0,即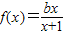 .
.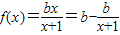 的图象关于点(-1,1)成中心对称,所以b=1,
的图象关于点(-1,1)成中心对称,所以b=1,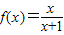 .
.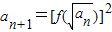 ,由(1)的结论开方得:
,由(1)的结论开方得: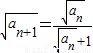 ,
,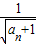 =
=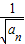 +1,所以
+1,所以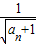 -
-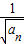 =1.
=1.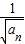 }是以1为首项,1为公差的等差数列.
}是以1为首项,1为公差的等差数列.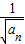 =1+(n-1)=n,即
=1+(n-1)=n,即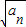 =
=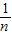 ,
,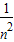 .
.

科目:高中数学 来源:2007-2008学年浙江省嘉兴一中高一(下)第一次月考数学试卷(解析版) 题型:解答题
 的图象过原点,且关于点(-1,1)成中心对称.
的图象过原点,且关于点(-1,1)成中心对称. ,求数列an的通项公式an.
,求数列an的通项公式an.查看答案和解析>>
科目:高中数学 来源:2013年四川省自贡市高考数学一模试卷(理科)(解析版) 题型:解答题
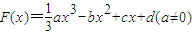 的图象过原点,f(x)=F′(x),g(x)=f′(x),f(1)=0,函数y=f(x)与y=g(x)的图象交于不同的两点A、B.
的图象过原点,f(x)=F′(x),g(x)=f′(x),f(1)=0,函数y=f(x)与y=g(x)的图象交于不同的两点A、B. ,求线段AB在x轴上的射影长的取值范围.
,求线段AB在x轴上的射影长的取值范围.查看答案和解析>>
科目:高中数学 来源:2012-2013学年贵州黔东南州高三第二次模拟(5月)考试文科数学试卷(解析版) 题型:填空题
已知函数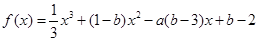 的图象过原点,且在原点处的切线斜率是
的图象过原点,且在原点处的切线斜率是 ,则不等式组
,则不等式组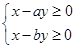 所确定的平面区域在
所确定的平面区域在 内的面积为 .
内的面积为 .
查看答案和解析>>
科目:高中数学 来源:2010年黑龙江省高二下学期期中考试数学(理) 题型:解答题
1.
(本小题满分10分)已知函数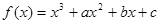 的图象过原点,且
的图象过原点,且 在
在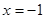 ,
, 处取得极值.
处取得极值.
(Ⅰ)求函数 的单调区间及极值;
的单调区间及极值;
(Ⅱ)若函数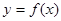 与
与 的图象有且仅有一个公共点,求实数
的图象有且仅有一个公共点,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com