练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数 ， ，其中a＞0，且a≠1．
    （1）若0＜a＜1，求满足不等式f（x）＜1的x的取值的集合；
    （2）求关于x的不等式f（x）≥g（x）的解的集合．

    【答案】
    （1）解：由不等式f（x）＜1，

    得

    因为0＜a＜1，所以3x2﹣3＞0，

    解得x＜﹣1，或x＞1，

    即所求解集为（﹣∞，﹣1）∪（1，+∞）


    （2）解：由不等式f（x）≥g（x）得

    （i）若0＜a＜1，则3x2﹣3≤﹣5x﹣5，

    即3x2+5x+2≤0，解得：

    （ii）若a＞1，则3x2﹣3≥﹣5x﹣5，

    即3x2+5x+2≥0，解得：

    综上，若0＜a＜1，所求解集为 ；

    若a＞1，所求解集为


    【解析】（1）根据a的范围，得到关于x的不等式，解出即可；（2）通过讨论a的范围，得到关于x的不等式，解出即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某房产开发商投资81万元建一座写字楼，第一年装修费为1万元，以后每年增加装修费2万元，现把写字楼出租，每年收入租金30万元．
    （1）若扣除投资和各种装修费，则从第几年开始获取纯利润？
    （2）若干年后开发商为了投资其他项目，有两种处理方案：
    ①年平均利润最大时，以50万元出售该楼；
    ②纯利润总和最大时，以10万元出售该楼；
    问选择哪种方案盈利更多？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数y=f（x）是R上的偶函数，对于任意x∈R，都有f（x+6）=f（x）+f（3）成立，当x1 ， x2∈[0，3]，且x1≠x2时，都有 ．给出下列命题： ①f（3）=0；
    ②直线x=﹣6是函数y=f（x）的图象的一条对称轴；
    ③函数y=f（x）在[﹣9，﹣6]上为增函数；
    ④函数y=f（x）在[﹣9，9]上有四个零点．
    其中所有正确命题的序号为（把所有正确命题的序号都填上）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】祖暅原理也就是“等积原理”，它是由我国南北朝杰出的数学家祖冲之的儿子祖暅首先提出来的，祖暅原理的内容是：夹在两个平行平面间的两个几何体，被平行于这两个平行平面的平面所截，如果截得两个截面的面积总相等，那么这两个几何体的体积相等．已知，两个平行平面间有三个几何体，分别是三棱锥、四棱锥、圆锥（高度都为），其中：三棱锥的底面是正三角形（边长为），四棱锥的底面是有一个角为的菱形（边长为），圆锥的体积为，现用平行于这两个平行平面的平面去截三个几何体，如果截得的三个截面的面积相等，那么，下列关系式正确的是（ ）

    A. B.

    C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在五面体ABCDEF中，四边形ABCD是边长为2的正方形，EF∥平面ABCD，EF=1，FB=FC，∠BFC=90°，AE= ，H是BC的中点．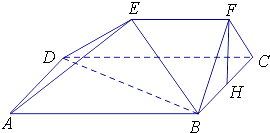

    （1）求证：FH∥平面BDE；
    （2）求证：AB⊥平面BCF；
    （3）求五面体ABCDEF的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义域为R的函数f（x）= 是奇函数．
    （1）求实数a，b的值；
    （2）判断并证明f（x）在（﹣∞，+∞）上的单调性；
    （3）若对任意实数t∈R，不等式f（kt2﹣kt）+f（2﹣kt）＜0恒成立，求k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知顶点在单位圆上的△ABC中，角A、B、C所对的边分别为a、b、c，且b2+c2=a2+bc．
    （1）求角A的大小；
    （2）若b2+c2=4，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C： =1（a＞b＞0）上的动点到焦点距离的最小值为 -1．以原点为圆心、椭圆的短半轴长为半径的圆与直线x﹣y+ =0相切．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）若过点M（2，0）的直线与椭圆C相交于A，B两点，P为椭圆上一点，且满足 + =t （O为坐标原点）．当|AB|= 时，求实数t的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合A={x|0＜ ≤1}，B={y|y=（ ）x ， 且x＜﹣1}
    （1）若集合C={x|x∈A∪B，且xA∩B}，求集合C；
    （2）设集合D={x|3﹣a＜x＜2a﹣1}，满足A∪D=A，求实数a的取值范围．

    查看答案和解析>>

    同步练习册答案