
分析 (Ⅰ)分别求出方盒的长、宽、高,求出方盒的体积即可;
(Ⅱ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的最大值即可.
解答 解:(Ⅰ)依题意,折成无盖方盒的长为a-2x、宽为$\frac{a}{2}-2x$、高为x,
故体积$y=V(x)=(a-2x)(\frac{a}{2}-2x)x=4{x^3}-3a{x^2}+\frac{a^2}{2}x,(0<x<\frac{a}{4})$,其中常数a>0;(5分)
(Ⅱ)由$y'=12{x^2}-6ax+\frac{a^2}{2}=0$(6分)得$x=\frac{{3±\sqrt{3}}}{12}a$,(7分)
在定义域内列极值分布表(10分)
| x | (0,$\frac{{3-\sqrt{3}}}{12}a$) | $\frac{{3-\sqrt{3}}}{12}a$ | $(\frac{{3-\sqrt{3}}}{12}a,\frac{a}{4})$ |
| f’(x) | + | 0 | - |
| f(x) | 单调增 | 极大值 | 单调减 |
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道中档题.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 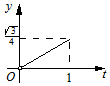 | B. | 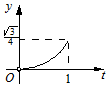 | C. | 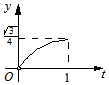 | D. | 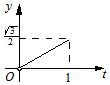 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com