[题目]已知点为坐标原点. 是椭圆上的两个动点.满足直线与直线关于直线对称.(1)证明直线的斜率为定值.并求出这个定值,(2)求的面积最大时直线的方程. 题目和参考答案——青夏教育精英家教网—

【题目】已知点为坐标原点，是椭圆上的两个动点，满足直线与直线关于直线对称.
（1）证明直线的斜率为定值，并求出这个定值；
（2）求的面积最大时直线的方程.

【答案】
（1）证明：设直线方程为：，代入得

设，因为点在椭圆上，所以

又由题知，直线的斜率与的斜率互为相反数，在上式中以代，可得
，
所以直线的斜率
故答案为:直线的斜率为定值，其值为
（2）解：由（1）可设直线方程为：，代入得
，则 .由可得 .
，到直线的距离，
可得，
当且仅当（满足），即时取等.
故答案为:直线的方程为：，或 .
【解析】(1)将直线方程代入椭圆方程中消去y得关于x的一元二次方程,由韦达定理得到两根和与积,由斜率公式求斜率;
(2)将三角形的面积表示为m的函数式,由二次函数求最值.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】某旅游爱好者计划从3个亚洲国家和3个欧洲国家中选择2个国家去旅游.
（Ⅰ）若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率；
（Ⅱ）若从亚洲国家和欧洲国家中各任选1个,求这2个国家包括但不包括的概率.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某校为调查高一、高二学生周日在家学习用时情况，随机抽取了高一、高二各人，对他们的学习时间进行了统计，分别得到了高一学生学习时间（单位：小时）的频数分布表和高二学生学习时间的频率分布直方图.

高一学生学习时间的频数分布表（学习时间均在区间内）：

学习时间
频数	3	1	8	4	2	2

高二学生学习时间的频率分布直方图：

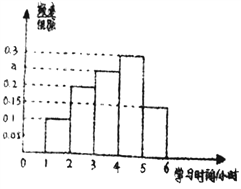
（1）求高二学生学习时间的频率分布直方图中的值，并根据此频率分布直方图估计该校高二学生学习时间的中位数；

（2）利用分层抽样的方法，从高一学生学习时间在，的两组里随机抽取人，再从这人中随机抽取人，求学习时间在这一组中至少有人被抽中的概率.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数y=f(x)，f(0)=-2，且对，y R，都有f(x+y)-f(y)=(x+2y+1)x.
（1）求f(x)的表达式；
（2）已知关于x的不等式f(x)-ax+a+1 的解集为A，若A[2,3]，求实数a的取值范围；
（3）已知数列{ }中，，，记，且数列{ 的前n项和为，
求证： .