
【题目】已知函数![]() .
.
(Ⅰ)若曲线![]() 在
在![]() 处的切线
处的切线![]() 与直线
与直线![]() 垂直,求直线
垂直,求直线![]() 的方程;
的方程;
(Ⅱ)当![]() 时,且
时,且![]() ,证明:
,证明:![]() .
.
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
【题目】将![]() 方格表的每个方格任意填入
方格表的每个方格任意填入![]() 或
或![]() ,然后允许进行如下操作:每次任意选择一行(或列),将这一行(或列)中的数全部变号.若无论开始时方格表的数怎样填,总能经过不超过
,然后允许进行如下操作:每次任意选择一行(或列),将这一行(或列)中的数全部变号.若无论开始时方格表的数怎样填,总能经过不超过![]() 次操作,使得方格表每一行中所有数的和、每一列中所有数的和均非负.试确定
次操作,使得方格表每一行中所有数的和、每一列中所有数的和均非负.试确定![]() 的最小值
的最小值![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心为坐标原点O,焦点在y轴上,离心率![]() ,椭圆上的点到焦点的最短距离为
,椭圆上的点到焦点的最短距离为![]() , 直线l与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且
, 直线l与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且![]() .
.
(1)求椭圆方程;
(2)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2-mlnx,h(x)=x2-x+a.
(1)当a=0时,f(x)≥h(x)在(1,+∞)上恒成立,求实数m的取值范围;
(2)当m=2时,若函数k(x)=f(x)-h(x)在区间(1,3)上恰有两个不同零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为抗击新冠病毒,某部门安排甲、乙、丙、丁、戊五名专家到三地指导防疫工作.因工作需要,每地至少需安排一名专家,其中甲、乙两名专家必须安排在同一地工作,丙、丁两名专家不能安排在同一地工作,则不同的分配方法总数为( )
A.18B.24C.30D.36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在校园篮球赛中,甲、乙两个队10场比赛的得分数据整理成如图所示的茎叶图,下列说法正确的是( )
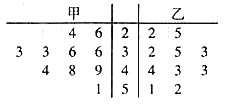
A.乙队得分的中位数是38.5
B.甲、乙两队得分在![]() 分数段频率相等
分数段频率相等
C.乙队的平均得分比甲队的高
D.甲队得分的稳定性比乙队好
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com