
(本小题共14分)
已知函数y=f(x), x![]() N*, y
N*, y![]() N*满足:
N*满足:
①对任意a,b![]() N*,a≠b,都有af(a)+bf(b)>af(b)+bf(a); ②对任意n
N*,a≠b,都有af(a)+bf(b)>af(b)+bf(a); ②对任意n![]() N*都有f [f(n)]=3n.
N*都有f [f(n)]=3n.
(Ⅰ)试证明:f(x)为N*上的单调增函数;
(Ⅱ)求f(1)+f(6)+f(28);
(Ⅲ)令an=f(3n),n![]() N*试证明:
N*试证明: ![]() ≤
≤![]() +…+
+…+![]() <
<![]() .
.
解:(Ⅰ)由①知,对任意a,b![]() N*,a<b,都有(a
N*,a<b,都有(a![]() b)(f (a)
b)(f (a)![]() f(b))>0,
f(b))>0,
由于a-b<0, 从而f(a)<f(b),所以函数f(x)为N*上的单调增函数. …3分
(Ⅱ)令f(1)=a,则a≥1,显然a≠1,否则f(f(1))= f(1)=1,与f(f(1))=3矛盾.,从而a>1,
而由f(f(1))=3,即得f(a)=3.
又由(Ⅰ)知f(a)>f(1)=a ,即a<3.
于是得1<a<3,又a![]() N*,从而a=2,即f(1)=2 ……………… 5分
N*,从而a=2,即f(1)=2 ……………… 5分
进而由f(a)=3知,f(2)=3.
于是f(3)=f(f(2))=3×2=6,………………………………… 7分
f(6)=f(f(3))=3×3=9,
f(9)=f(f(6))=3×6=18,
f(18)=f(f(9))=3×9=27,
f(27)=f(f(18))=3×18=54,
f(54)=f(f(27))=3×27=81.
由于54![]() 27=81
27=81![]() 54=27,
54=27,
而且由(Ⅰ)知,函数f(x)为单调增函数,因此f(28)=54+1=55.
从而f(1)+f(6)+f(28)=2+9+55=66.……………………… 9分
(Ⅲ)f(an)=f(f(3n))=3×3n=3n+1,
an+1=f(3n+1)=f(f(an))=3an,a1=f(3)=6.
即数列{an}是以6为首项,以3为公比的等比数列.
∴an=6×3n![]() 1=2×3n(n=1,2,3…).………………………… 11分
1=2×3n(n=1,2,3…).………………………… 11分
于是![]() +
+![]() +…+
+…+![]() =
=![]() (
(![]() +
+![]() +…+
+…+![]() )=
)=![]() ×
× .
.
显然![]() (
(![]() )<
)<![]() .………………………………………………12分
.………………………………………………12分
另一方面3n=(1+2)n=1+![]() ×2+
×2+![]() ×22+…+
×22+…+![]() ×2n≥1+2n,
×2n≥1+2n,
从而![]() (1
(1![]()
![]() )≥
)≥![]() (1
(1![]()
![]() )=
)=![]() .
.
综上得![]() ≤
≤![]() +
+![]() +…+
+…+![]() <
<![]() .…………………………14分
.…………………………14分
说明:其他正确解法按相应步骤给分.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
(本小题共14分)
如图,四棱锥![]() 的底面是正方形,
的底面是正方形,![]() ,点E在棱PB上。
,点E在棱PB上。
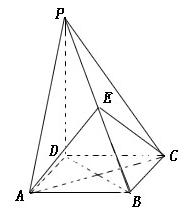
(Ⅰ)求证:平面![]() ;
;
(Ⅱ)当![]() 且E为PB的中点时,求AE与平面PDB所成的角的大小。
且E为PB的中点时,求AE与平面PDB所成的角的大小。
查看答案和解析>>
科目:高中数学 来源: 题型:
(2009北京理)(本小题共14分)
已知双曲线![]() 的离心率为
的离心率为![]() ,右准线方程为
,右准线方程为![]()
(Ⅰ)求双曲线![]() 的方程;
的方程;
(Ⅱ)设直线![]() 是圆
是圆![]() 上动点
上动点![]() 处的切线,
处的切线,![]() 与双曲线
与双曲线![]() 交
交
于不同的两点![]() ,证明
,证明![]() 的大小为定值.
的大小为定值.
查看答案和解析>>
科目:高中数学 来源:2013届度广东省高二上学期11月月考理科数学试卷 题型:解答题
(本小题共14分)在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD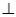 底面ABCD,PD=DC,点E是PC的中点,作EF
底面ABCD,PD=DC,点E是PC的中点,作EF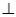 PB交PB于点F
PB交PB于点F
⑴求证:PA//平面EDB
⑵求证:PB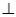 平面EFD
平面EFD
⑶求二面角C-PB-D的大小

查看答案和解析>>
科目:高中数学 来源:2010年北京市崇文区高三下学期二模数学(文)试题 题型:解答题
(本小题共14分)
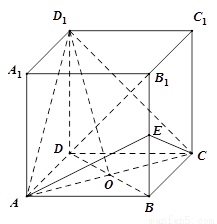
正方体 的棱长为
的棱长为 ,
, 是
是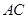 与
与 的交点,
的交点, 为
为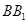 的中点.
的中点.
(Ⅰ)求证:直线 ∥平面
∥平面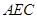 ;
;
(Ⅱ)求证: 平面
平面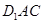 ;
;
(Ⅲ)求三棱锥 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com