
【题目】回答下列两个问题, 并给出例子或证明.
(1)对任意正整数![]() , 在平面上是否都存在
, 在平面上是否都存在![]() 个不在同一条直线上的点, 使得任意两点间的距离都为正整数?
个不在同一条直线上的点, 使得任意两点间的距离都为正整数?
(2)在平面上是否存在两两不同的无限点列组成的点集![]() , 使得
, 使得![]() 内所有点不在同一条直线上, 且
内所有点不在同一条直线上, 且![]() 内任意两点间的距离为正整数?
内任意两点间的距离为正整数?
【答案】(1)存在.(2)不存在
【解析】
(1)存在.
对于任意的![]() (
(![]() ),取互不相同的
),取互不相同的![]() 个质数
个质数![]() .
.
令![]() ,
,
显然,![]() .
.
令![]() ,
,
于是,![]() .
.
在![]() 轴上取点
轴上取点![]() ,在
,在![]() 轴上取点
轴上取点![]() ,
,
易知,这![]() 个点
个点![]() ,
,![]() 不在同一条直线上,且
不在同一条直线上,且
![]() 为整数
为整数![]() .
.
故![]() 为整数.
为整数.
(2)不存在.
若不然, 假设存在不共线的无限点列组成的点集![]() ,且
,且![]() 内任意两点间的距离都为正整数.取不共线的三点
内任意两点间的距离都为正整数.取不共线的三点![]() ∈
∈![]() , 注意到,
, 注意到,![]() 到
到![]() 之间的整数值.
之间的整数值.
而一![]() 到
到![]() 之间的整数值总共只有有限个,
之间的整数值总共只有有限个,
由双曲线定义可知, ![]() 内除去
内除去![]() 三点的其余无限多个点必在以点A 和点B 为两个焦点的有限条互不相交的双曲线上, 称它们为AB 族双曲线.
三点的其余无限多个点必在以点A 和点B 为两个焦点的有限条互不相交的双曲线上, 称它们为AB 族双曲线.
同理, ![]() 内除去
内除去![]() 三点的其余无限多个点必在以点B 和点C 为两个焦点的有限条互不相交的双曲线上, 称它们为BC族双曲线.
三点的其余无限多个点必在以点B 和点C 为两个焦点的有限条互不相交的双曲线上, 称它们为BC族双曲线.
由于![]() 三点不共线, 故两族双曲线的交点显然只有有限个.
三点不共线, 故两族双曲线的交点显然只有有限个.
然而,![]() 内除去
内除去![]() 三点的其余无限多个点中的每个点既在AB 族双曲线上,
三点的其余无限多个点中的每个点既在AB 族双曲线上,
又在BC 族双曲线上,从而, 必在两族双曲线的交点上.而两族双曲线的交点个数有限, 矛盾.


科目:高中数学 来源: 题型:
【题目】(1)6个人按下列要求站一横排,甲、乙必须相邻,有多少种不同的站法?
(2)6个人按下列要求站一横排,甲不站左端,乙不站右端.有多少种不同的站法?
(3)用0,1,2,3,4,5这六个数字可以组成多少个六位数且是奇数(无重复数字的数)?
(4)用0,1,2,3,4,5这六个数字可以组成多少个个位上的数字不是5的六位数(无重复数字的数)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f1(x),y=f2(x),定义函数f(x)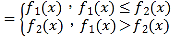 .
.
(1)设函数f1(x)=x+3,f2(x)=x2﹣x,求函数y=f(x)的解析式;
(2)在(1)的条件下,g(x)=mx+2(m∈R),函数h(x)=f(x)﹣g(x)有三个不同的零点,求实数m的取值范围;
(3)设函数f1(x)=x2﹣2,f2(x)=|x﹣a|,函数F(x)=f1(x)+f2(x),求函数F(x)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某亲子公园拟建议广告牌,将边长为![]() 米的正方形ABCD和边长为1米的正方形AEFG在A点处焊接,AM、AN、GM、DN均用加强钢管支撑,其中支撑钢管GM、DN垂直于地面于M点和N点,且GM、DN、MN长度相等
米的正方形ABCD和边长为1米的正方形AEFG在A点处焊接,AM、AN、GM、DN均用加强钢管支撑,其中支撑钢管GM、DN垂直于地面于M点和N点,且GM、DN、MN长度相等![]() 不计焊接点大小
不计焊接点大小![]()

![]() 若
若![]() 时,求焊接点A离地面距离;
时,求焊接点A离地面距离;
![]() 若记
若记![]() ,求加强钢管AN最长为多少?
,求加强钢管AN最长为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com