
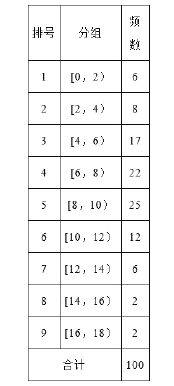
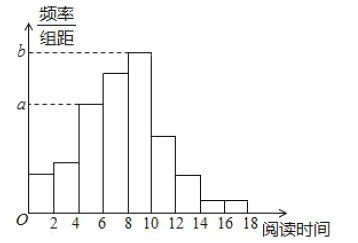
【题目】从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:
(Ⅰ)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的概率;
(Ⅱ)求频率分布直方图中的![]() 的值;
的值;
(Ⅲ)从阅读时间在![]() 的学生中任选2人,求恰好有1人阅读时间在
的学生中任选2人,求恰好有1人阅读时间在![]() ,另1 人阅读时间在
,另1 人阅读时间在![]() 的概率.
的概率.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】试题分析:(1)利用频率估计概率,由频率分布直方图得课外阅读不少于12小时的学生数,然后除以100即可;(2)利用![]() 进行求解,可得
进行求解,可得![]() ;(3)由频率分布直方图可得阅读时间在
;(3)由频率分布直方图可得阅读时间在![]() 的学生共4人,其中阅读时间落在
的学生共4人,其中阅读时间落在![]() 的有2人,阅读时间落在
的有2人,阅读时间落在![]() 的有2人,用列举法得到所有可能的试验结果,根据古典概型概率公式求解。
的有2人,用列举法得到所有可能的试验结果,根据古典概型概率公式求解。
试题解析:
(1)由频率分布直方图知,100名学生中课外阅读不少于12小时的学生共有10名,所以样本中课外阅读时间少于12小时的的频率是![]() .
.
(2)课外阅读时间落在![]() 的有17人,频率为0.17,
的有17人,频率为0.17,
所以![]()
课外阅读时间落在![]() 的有25人,频率为0.25,
的有25人,频率为0.25,
所以![]()
(3)课外阅读时间落在![]() 的有2人设为
的有2人设为![]() ;课外阅读时间落在
;课外阅读时间落在![]() 的有2人设为
的有2人设为![]() ,
,
则从课外阅读时间落在![]() 的学生中任选2人包含
的学生中任选2人包含![]() 共 6 种,
共 6 种,
其中恰好有1人阅读时间在![]() ,另1人阅读时间在
,另1人阅读时间在![]() 的有
的有![]() 共 4 种,
共 4 种,
所以所求概率为![]() ,
,
即恰好有1人阅读时间在![]() ,另1 人阅读时间在
,另1 人阅读时间在![]() 的概率为
的概率为![]() .
.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:
【题目】某车间共有![]() 名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.

(Ⅰ) 根据茎叶图计算样本均值;
(Ⅱ) 日加工零件个数大于样本均值的工人为优秀工人,根据茎叶图推断该车间![]() 名工人中有几名优秀工人;
名工人中有几名优秀工人;
(Ⅲ) 从该车间![]() 名工人中,任取2人,求恰有1名优秀工人的概率.
名工人中,任取2人,求恰有1名优秀工人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的焦点
的焦点![]() 、
、![]() 在
在![]() 轴上,且椭圆
轴上,且椭圆![]() 经过
经过![]() ,过点
,过点![]() 的直线
的直线![]() 与
与![]() 交于点
交于点![]() ,与抛物线
,与抛物线![]() :
: ![]() 交于
交于![]() 、
、![]() 两点,当直线
两点,当直线![]() 过
过![]() 时
时![]() 的周长为
的周长为![]() .
.
(Ⅰ)求![]() 的值和
的值和![]() 的方程;
的方程;
(Ⅱ)以线段![]() 为直径的圆是否经过
为直径的圆是否经过![]() 上一定点,若经过一定点求出定点坐标,否则说明理由。
上一定点,若经过一定点求出定点坐标,否则说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是某校高三一次月考5个班级的数学、物理的平均成绩:
班级 | 1 | 2 | 3 | 4 | 5 |
数学( | 111 | 113 | 119 | 125 | 127 |
物理( | 92 | 93 | 96 | 99 | 100 |
(Ⅰ)一般来说,学生的物理成绩与数学成绩具有线性相关关系,根据上表提供的数据,求两个变量![]() ,
, ![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)从以上5个班级中任选两个参加某项活动,设选出的两个班级中数学平均分在115分以上的个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:  ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
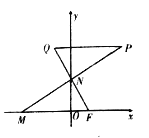
【题目】已知点![]() ,动点
,动点![]() ,
, ![]() 分别在
分别在![]() 轴,
轴, ![]() 轴上运动,
轴上运动, ![]() ,
, ![]() 为平面上一点,
为平面上一点, ![]() ,过点
,过点![]() 作
作![]() 平行于
平行于![]() 轴交
轴交![]() 的延长线于点
的延长线于点![]() .
.
(Ⅰ)求点![]() 的轨迹曲线
的轨迹曲线![]() 的方程;
的方程;
(Ⅱ)过![]() 点作
点作![]() 轴的垂线
轴的垂线![]() ,平行于
,平行于![]() 轴的两条直线
轴的两条直线![]() ,
, ![]() 分别交曲线
分别交曲线![]() 于
于![]() ,
, ![]() 两点(直线
两点(直线![]() 不过
不过![]() ),交
),交![]() 于
于![]() ,
, ![]() 两点.若线段
两点.若线段![]() 中点的轨迹方程为
中点的轨迹方程为![]() ,求
,求![]() 与
与![]() 的面积之比.
的面积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是某校高三一次月考5个班级的数学、物理的平均成绩:
班级 | 1 | 2 | 3 | 4 | 5 |
数学( | 111 | 113 | 119 | 125 | 127 |
物理( | 92 | 93 | 96 | 99 | 100 |
(Ⅰ)一般来说,学生的物理成绩与数学成绩具有线性相关关系,根据上表提供的数据,求两个变量![]() ,
, ![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)从以上5个班级中任选两个参加某项活动,设选出的两个班级中数学平均分在115分以上的个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:  ,
, ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com