
某地政府鉴于某种日常食品价格增长过快,欲将这种食品价格控制在适当范围内,决定对这种食品生产厂家提供政府补贴,设这种食品的市场价格为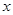 元/千克,政府补贴为
元/千克,政府补贴为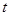 元/千克,根据市场调查,当
元/千克,根据市场调查,当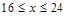 时,这种食品市场日供应量
时,这种食品市场日供应量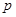 万千克与市场日需量
万千克与市场日需量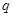 万千克近似地满足关系:
万千克近似地满足关系: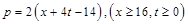 ,
,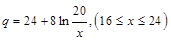 。当
。当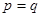 市场价格称为市场平衡价格。
市场价格称为市场平衡价格。
(1)将政府补贴表示为市场平衡价格的函数,并求出函数的值域;
(2)为使市场平衡价格不高于每千克20元,政府补贴至少为每千克多少元?
(1)值域为[ + ln
+ ln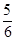 ,
,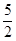 + ln
+ ln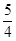 ];
];
(2)要使市场平衡价格不高于每千克20元,政府补贴至少为1.5元/千克。
解析试题分析:(1)由P=Q得2(x + 4t -14 )= 24+8ln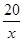 (16≤x≤24 ,t>0)。
(16≤x≤24 ,t>0)。
t= -
-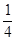 x+ ln
x+ ln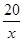 (16≤x≤24)。 3分
(16≤x≤24)。 3分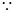 t′=-
t′=-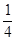 -
- <0,
<0,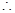 t是x的减函数。
t是x的减函数。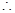 tmin=
tmin= -
-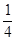
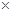 24+ ln
24+ ln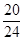 =
= +ln
+ln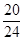 =
= + ln
+ ln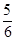 ; 5分
; 5分
tmax= -
-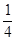
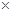 16+ ln
16+ ln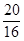 =
=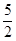 + ln
+ ln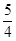 ,
, 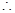 值域为[
值域为[ + ln
+ ln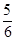 ,
,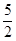 + ln
+ ln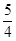 ] 7分
] 7分
(2)由(1) t= -
-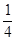 x+ ln
x+ ln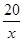 (16≤x≤24)。
(16≤x≤24)。
而x=20时,t= -
-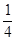
 20 + ln
20 + ln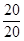 =1.5(元/千克) 9分
=1.5(元/千克) 9分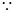 t是x的减函数。欲使x
t是x的减函数。欲使x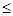 20,必须t
20,必须t 1.5(元/千克)
1.5(元/千克)
要使市场平衡价格不高于每千克20元,政府补贴至少为1.5元/千克。……12分
考点:本题主要考查函数模型,运用的是研究函数的单调性及最值。
点评:典型题,应用问题在高考命题中占有的份额越来越稳定,一般是“一大两小”或“两大一小”,作为函数模型的考查,基本比较稳定。解题过程中,要遵循“审清题意、构建函数、求解函数、写出答案”等步骤。


科目:高中数学 来源: 题型:解答题
经市场调查:生产某产品需投入年固定成本为3万元,每生产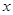 万件,需另投入流动成本为
万件,需另投入流动成本为 万元,在年产量不足8万件时,
万元,在年产量不足8万件时,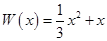 (万元),在年产量不小于8万件时,
(万元),在年产量不小于8万件时,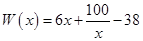 (万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.
(万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.
(1)写出年利润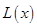 (万元)关于年产量
(万元)关于年产量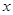 (万件)的函数解析式;
(万件)的函数解析式;
(注:年利润=年销售收入 固定成本
固定成本 流动成本)
流动成本)
(2)年产量为多少万件时,在这一商品的生产中所获利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某单位决定对本单位职工实行年医疗费用报销制度,拟制定年医疗总费用在2万元至10万元(包括2万元和10万元)的报销方案,该方案要求同时具备下列三个条件:①报销的医疗费用y(万元)随医疗总费用x(万元)增加而增加;②报销的医疗费用不得低于医疗总费用的50%;③报销的医疗费用不得超过8万元.
(1)请你分析该单位能否采用函数模型y=0.05(x2+4x+8)作为报销方案;
(2)若该单位决定采用函数模型y=x-2lnx+a(a为常数)作为报销方案,请你确定整数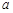 的值.(参考数据:ln2»0.69,ln10»2.3)
的值.(参考数据:ln2»0.69,ln10»2.3)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在某服装批发市场,某种品牌的时装当季节将来临时,价格呈上升趋势,设这种时装开始时定价为20元,并且每周(7天)涨价2元,从第6周开始保持30元的价格平稳销售;从第12周开始,当季节即将过去时,平均每周减价2元,直到第16周周末,该服装不再销售。
⑴试建立销售价y与周次x之间的函数关系式;
⑵若这种时装每件进价Z与周次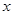 次之间的关系为Z=
次之间的关系为Z=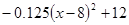 ,1≤
,1≤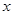 ≤16,且
≤16,且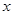 为整数,试问该服装第几周出售时,每件销售利润最大?最大利润为多少?
为整数,试问该服装第几周出售时,每件销售利润最大?最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商场销售某种商品的经验表明,该商品每日的销售量y (单位:千克)与销售价格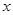 (单位:元/千克)满足关系式y=
(单位:元/千克)满足关系式y=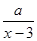 +10(x-6)2,其中3<x<6,a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
+10(x-6)2,其中3<x<6,a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
(1)求a的值;
(2)若该商品的成品为3元/千克, 试确定销售价格x的值, 使商场每日销售该商品所获得的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某商品每件成本9元,售价为30元,每星期卖出432件,如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值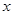 (单位:元,
(单位:元,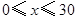 )的平方成正比,已知商品单价降低2元时,一星期多卖出24件.(I)将一个星期的商品销售利润表示成
)的平方成正比,已知商品单价降低2元时,一星期多卖出24件.(I)将一个星期的商品销售利润表示成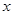 的函数;(II)如何定价才能使一个星期的商品销售利润最大?
的函数;(II)如何定价才能使一个星期的商品销售利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
有甲、乙两种商品,经营销售这两种商品所能获得的利润依次是 (万元)和
(万元)和 (万元),它们与投入资金
(万元),它们与投入资金 (万元)的关系有经验公式:
(万元)的关系有经验公式: 。今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少?能获得最大利润是多少?
。今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少?能获得最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com