
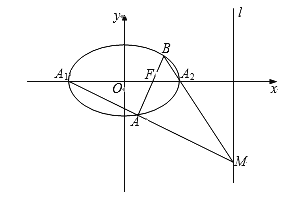
【题目】如图,已知椭圆C:![]() 的左、右顶点分别为
的左、右顶点分别为![]() 右焦点为
右焦点为![]() ,右准线l的方程为
,右准线l的方程为![]() ,过焦点F的直线与椭圆C相交于点A,B(不与点
,过焦点F的直线与椭圆C相交于点A,B(不与点![]() 重合).
重合).
(1)求椭圆C的标准方程;
(2)当直线AB的倾斜角为45°时,求弦AB的长;
(3)设直线![]() 交l于点M,求证:B,
交l于点M,求证:B,![]() ,M三点共线.
,M三点共线.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 、抛物线
、抛物线![]() 的焦点均在
的焦点均在![]() 轴上,
轴上,![]() 的中心和
的中心和![]() 的顶点均为原点
的顶点均为原点![]() ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
| 3 |
| 4 |
|
|
| 0 |
|
|
(Ⅰ)求![]() 的标准方程;
的标准方程;
(Ⅱ)请问是否存在直线![]() 满足条件:①过
满足条件:①过![]() 的焦点
的焦点![]() ;②与
;②与![]() 交不同两点
交不同两点![]() 且满足
且满足![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人投篮的命中率各不相同,其中乙的命中率是甲的2倍,丙的命中率等于甲与乙的命中率之和.若甲与乙各投篮一次,每人投篮相互独立,则他们都命中的概率为0.18.
(1)求甲、乙、丙三人投篮的命中率;
(2)现要求甲、乙、丙三人各投篮一次,假设每人投篮相互独立,记三人命中总次数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 的顶点
的顶点![]() ,
,![]() ,且
,且![]() 、
、![]() 、
、![]() 成等差数列.
成等差数列.
(1)求![]() 的顶点
的顶点![]() 的轨迹方程;
的轨迹方程;
(2)直线![]() 与顶点
与顶点![]() 的轨迹交于
的轨迹交于![]() 两点,当线段
两点,当线段![]() 的中点
的中点![]() 落在直线
落在直线![]() 上时,试问:线段
上时,试问:线段![]() 的垂直平分线是否恒过定点?若过定点,求出定点的坐标;若不过定点,请说明理由.
的垂直平分线是否恒过定点?若过定点,求出定点的坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】跨年迎新联欢晚会简称跨年晚会,是指每年阳历年末12月31日晚上各电视台和政府为喜迎新而精心策划的演唱会活动,跨年晚会首次出现在港台地区,跨年晚会因形式和举办地不同因而名称也不同,如央视启航2020跨年盛典,湖南卫视跨年演唱会,东方卫视迎新晚会等.某电视台为了了解2020年举办的跨年迎新晚会观众的满意度,现分别随机选出![]() 名观众对迎新晚会的质量评估评分,最高分为
名观众对迎新晚会的质量评估评分,最高分为![]() 分,综合得分情况如下表所示:
分,综合得分情况如下表所示:
综合得分 |
|
|
|
|
|
|
|
观众人数 | 5 | 10 | 25 | 30 | 15 | 10 | 5 |
根据表中的数据,回答下列问题:
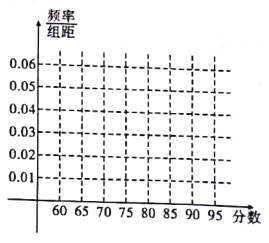
(1)根据表中的数据,绘制这![]() 位观众打分的频率分布直方图;
位观众打分的频率分布直方图;
(2)已知观众的评分![]() 近似服从
近似服从![]() ,其中
,其中![]() 是反应随机变量
是反应随机变量![]() 取值的平均水平的特征数,工作人员在分析数据时发现,可用
取值的平均水平的特征数,工作人员在分析数据时发现,可用![]() 位观众评分的平均数估计
位观众评分的平均数估计![]() ,但由于评分观众人数较少,误差较大,所以不能直接用
,但由于评分观众人数较少,误差较大,所以不能直接用![]() 位观众评分的标准差的值估计
位观众评分的标准差的值估计![]() ,而在这
,而在这![]() 位观众打分的频率分布直方图的基础上依据
位观众打分的频率分布直方图的基础上依据![]() 来估计
来估计![]() 更科学合理,试求
更科学合理,试求![]() 和
和![]() 的估计值(
的估计值(![]() 的结果精确到小数点后两位).
的结果精确到小数点后两位).
查看答案和解析>>
科目:高中数学 来源: 题型:
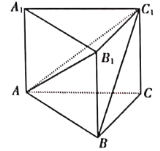
【题目】《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1000多年,在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵(qian du);阳马指底面为矩形,一侧棱垂直于底面的四棱锥,鳖膈(bie nao)指四个面均为直角三角形的四面体.如图在堑堵![]() 中,
中,![]() ,
,![]() .给出下列四个结论:
.给出下列四个结论:
①四棱锥![]() 为阳马;
为阳马;
②直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ;
;
③当![]() 时,异面直线
时,异面直线![]() 与
与![]() 所成的角的余弦值为
所成的角的余弦值为![]() ;
;
④当三棱锥![]() 体积最大时,四棱锥
体积最大时,四棱锥![]() 的外接球的表面积为
的外接球的表面积为![]() .
.
其中,所有正确结论的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下:

等级 | 不合格 | 合格 | ||
得分 |
|
|
|
|
频数 | 6 | a | 24 | b |
(1)由该题中频率分布直方图求测试成绩的平均数和中位数;
(2)其他条件不变在评定等级为“合格”的学生中依次抽取2人进行座谈,每次抽取1人,求在第1次抽取的测试得分低于80分的前提下,第2次抽取的测试得分仍低于80分的概率;
(3)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中抽取10人进行座谈.现再从这10人中任选4人,记所选4人的量化总分为![]() ,求
,求![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为
中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() ,曲线C的极坐标方程为
,曲线C的极坐标方程为![]() .
.
(Ⅰ)求直线l和曲线C的直角坐标方程;
(Ⅱ)点M为曲线C上一点,求M到直线l的最小距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com