
【题目】若将函数y=2sin(3x+φ)的图象向右平移 ![]() 个单位后得到的图象关于点(
个单位后得到的图象关于点( ![]() )对称,则|φ|的最小值是( )
)对称,则|φ|的最小值是( )
A.![]()
B.![]()
C.![]()
D.![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知动圆M恒过点(0,1),且与直线y=﹣1相切.
(1)求圆心M的轨迹方程;
(2)动直线l过点P(0,﹣2),且与点M的轨迹交于A、B两点,点C与点B关于y轴对称,求证:直线AC恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为奇函数,
为奇函数, ![]() 为偶函数,且
为偶函数,且![]() .
.
(1)求![]() 及
及![]() 的解析式及定义域;
的解析式及定义域;
(2)若关于![]() 的不等式
的不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(3)如果函数![]() ,若函数
,若函数![]() 有两个零点,求实数
有两个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形![]() 是正方形,
是正方形, ![]() 平面
平面![]() ,
, ![]() 分别为
分别为![]() 的中点,且
的中点,且![]() .
.
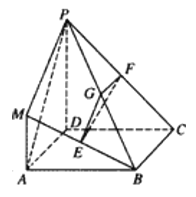
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 与四棱锥
与四棱锥![]() 的体积之比.
的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(Ⅰ)求a,b的值;
(Ⅱ)已知f(x)在定义域上为减函数,若对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0(k为常数)恒成立.求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等比数列,a1=2,且a1 , a3+1,a4成等差数列.
(1)求数列{an}的通项公式;
(2)若bn=log2an , 求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系 ![]() 中,以原点O为极点,x轴的非负半轴为极轴建立极坐标系,直线
中,以原点O为极点,x轴的非负半轴为极轴建立极坐标系,直线 ![]() 的极坐标方程是
的极坐标方程是 ![]() ,圆
,圆 ![]() 的极坐标方程是
的极坐标方程是 ![]() .
.
(1)求 ![]() 与
与 ![]() 交点的极坐标;
交点的极坐标;
(2)设 ![]() 为
为 ![]() 的圆心,
的圆心, ![]() 为
为 ![]() 与
与 ![]() 交点连线的中点,已知直线
交点连线的中点,已知直线 ![]() 的参数方程是
的参数方程是  (
( ![]() 为参数),求
为参数),求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市出租车的收费标准是:3千米以内(含3千米),收起步价8元;3千米以上至8千米以内(含8千米),超出3千米的部分按![]() 元/千米收取;8千米以上,超出8千米的部分按2元/千米收取.
元/千米收取;8千米以上,超出8千米的部分按2元/千米收取.
(1)计算某乘客搭乘出租车行驶7千米时应付的车费;
(2)试写出车费![]() (元)与里程
(元)与里程![]() (千米)之间的函数解析式并画出图像;
(千米)之间的函数解析式并画出图像;

(3)小陈周末外出,行程为10千米,他设计了两种方案:
方案1:分两段乘车,先乘一辆行驶5千米,下车换乘另一辆车再行5千米至目的地
方案2:只乘一辆车至目的地,试问:以上哪种方案更省钱,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 为定义在
为定义在 ![]() 上的偶函数,当
上的偶函数,当 ![]() 时,有
时,有 ![]() ,且当
,且当 ![]() 时,
时, ![]() ,给出下列命题:
,给出下列命题:
① ![]() 的值为
的值为 ![]() ;
;
②函数 ![]() 在定义域上为周期是2的周期函数;
在定义域上为周期是2的周期函数;
③直线 ![]() 与函数
与函数 ![]() 的图像有1个交点;
的图像有1个交点;
④函数 ![]() 的值域为
的值域为 ![]() .
.
其中正确的命题序号有 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com