
【题目】五个人站成一排,求在下列条件下的不同排法种数:
(1)甲必须在排头;
(2)甲、乙相邻;
(3)甲不在排头,并且乙不在排尾;
(4)其中甲、乙两人自左向右从高到矮排列且互不相邻
【答案】
(1)
【解答】解:特殊元素是甲,特殊位置是排头;首先排“排头”不动,再排其它4个位置有![]() 种,所以共有:
种,所以共有:![]() 种
种
(2)
【解答】解:把甲、乙看成一个人来排有 ![]() 种,而甲、乙也存在顺序变化,所以甲、乙相邻排法种数为
种,而甲、乙也存在顺序变化,所以甲、乙相邻排法种数为![]() 种
种
(3)
【解答】解:甲不在排头,并且乙不在排尾排法种数为:![]() 种
种
(4)
【解答】解:先将其余3个全排列![]() ,再将甲、乙插入4个空位
,再将甲、乙插入4个空位![]() ,所以,一共有
,所以,一共有![]() 种不同排法
种不同排法
【解析】本题主要考查了,解决问题的关键是(1)特殊元素(位置)法:首先排“排头”不动,再排其它4个位置有 ![]() 种共有24种;(2)捆绑法:把甲、乙看成一个人来排有
种共有24种;(2)捆绑法:把甲、乙看成一个人来排有 ![]() 种,而甲、乙也存在顺序变化,所以甲、乙相邻排法种数为
种,而甲、乙也存在顺序变化,所以甲、乙相邻排法种数为 ![]() 种;(3)对立法:甲在排头和乙在排尾的各
种;(3)对立法:甲在排头和乙在排尾的各 ![]() 种,其中甲在排头且乙在排尾的有
种,其中甲在排头且乙在排尾的有![]() 种,五个人站成一排的不同排法数是
种,五个人站成一排的不同排法数是![]() 种,所以甲不在排头,并且乙不在排尾的有
种,所以甲不在排头,并且乙不在排尾的有 ![]() 种;(4)插空法:先将其余3个全排列
种;(4)插空法:先将其余3个全排列 ![]() 种,再将甲、乙插入4个空位
种,再将甲、乙插入4个空位 ![]() 种, 所以,一共有
种, 所以,一共有 ![]() 种不同排法.
种不同排法.


科目:高中数学 来源: 题型:
【题目】若二次函数 ![]() 的图象和直线y=x无交点,现有下列结论:
的图象和直线y=x无交点,现有下列结论:
①方程f[f(x)]=x一定没有实数根;
②若a>0,则不等式f[f(x)]>x对一切实数x都成立;
③若a<0,则必存存在实数x0 , 使f[f(x0)]>x0;
④若a+b+c=0,则不等式f[f(x)]<x对一切实数都成立;
⑤函数 ![]() 的图象与直线y=﹣x也一定没有交点.
的图象与直线y=﹣x也一定没有交点.
其中正确的结论是(写出所有正确结论的编号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,椭圆C截直线y=1所得线段的长度为
,椭圆C截直线y=1所得线段的长度为![]() .
.
(Ⅰ)求椭圆C的方程;
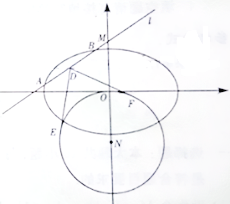
(Ⅱ)动直线l:y=kx+m(m≠0)交椭圆C于A,B两点,交y轴于点M.点N是M关于O的对称点,⊙N的半径为|NO|. 设D为AB的中点,DE,DF与⊙N分别相切于点E,F,求![]() EDF的最小值.
EDF的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=3,an+1=can+m(c,m为常数)
(1)当c=1,m=1时,求数列{an}的通项公式an;
(2)当c=2,m=﹣1时,证明:数列{an﹣1}为等比数列;
(3)在(2)的条件下,记bn= ![]() ,Sn=b1+b2+…+bn , 证明:Sn<1.
,Sn=b1+b2+…+bn , 证明:Sn<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某种信息传输过程中,用4个数字的一个排列(数字允许重复)表示一个信息,不同排列表示不同信息.若所用数字只有0和1,则与信息0110至多有两个对应位置上的数字相同的信息个数为 ( )
A.10
B.11
C.12
D.15
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司利用简单随机抽样方法,对投保车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:
赔付金额(元) | 0 | 1 000 | 2 000 | 3 000 | 4 000 |
车辆数(辆) | 500 | 130 | 100 | 150 | 120 |
(1)若每辆车的投保金额均为2800元,估计赔付金额大于投保金额的概率.
(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直棱柱ABC﹣A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB= ![]() AB. (Ⅰ)证明:BC1∥平面A1CD;
AB. (Ⅰ)证明:BC1∥平面A1CD;
(Ⅱ)求二面角D﹣A1C﹣E的余弦值.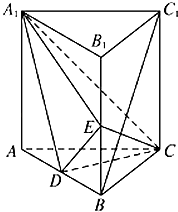
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com