
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,短轴的一个端点为
,短轴的一个端点为![]() .过椭圆左顶点
.过椭圆左顶点![]() 的直线
的直线![]() 与椭圆的另一交点为
与椭圆的另一交点为![]() .
.
(1)求椭圆的方程;
(2)若![]() 与直线
与直线![]() 交于点
交于点![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
【题目】一个盒子里装有三张卡片,分别标记有数字1,2,3,这三张卡片除标记的数字外完全相同.随机有放回地抽取3次,每次抽取1张,将抽取的卡片上的数字依次记为a,b,c.求:
(1)“抽取的卡片上的数字满足a+b=c”的概率;
(2)“抽取的卡片上的数字a,b,c不完全相同”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,给当地人民造成了巨大的财产损失,适逢暑假,小张调查了当地某小区的100户居民由于台风造成的经济损失,将收集的数据分成![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 五组,并作出如下频率分布直方图(图1):
五组,并作出如下频率分布直方图(图1):
(Ⅰ)台风后居委会号召小区居民为台风重灾区捐款,小张调查的100户居民捐款情况如右下表格,在图2表格空白处填写正确数字,并说明是否有![]() 以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?


(Ⅱ)将上述调查所得到的频率视为概率. 现在从该地区大量受灾居民中,采用随机抽样方法每次抽取1户居民,抽取3次,记被抽取的3户居民中自身经济损失超过4000元的人数为![]() . 若每次抽取的结果是相互独立的,求
. 若每次抽取的结果是相互独立的,求![]() 的分布列,期望
的分布列,期望![]() 和方差
和方差![]() .
.
附:临界值表
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
随机量变

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是__________.(写出所有正确命题的序号)
①已知![]() ,“
,“![]() 且
且![]() ”是“
”是“![]() ”的充要条件;
”的充要条件;
②已知平面向量![]() ,“
,“![]() 且
且![]() ”是“
”是“![]() ”的必要不充分条件;
”的必要不充分条件;
③已知![]() ,“
,“![]() ”是“
”是“![]() ”的充分不必要条件;
”的充分不必要条件;
④命题![]() :“
:“![]() ,使
,使![]() 且
且![]() ”的否定为
”的否定为![]() :“
:“![]() ,都有
,都有![]() 且
且![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下列表:
喜爱打篮球 | 不喜爱打篮球 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知在全班50人中随机抽取1人,抽到喜爱打篮球的学生的概率为![]() .
.
(1)请将上表补充完整(不用写计算过程);
(2)能否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由.
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: 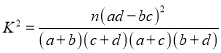 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一张半径为4的圆形纸片的圆心为![]() ,
, ![]() 是圆内一个定点,且
是圆内一个定点,且![]() ,
, ![]() 是圆上一个动点,把纸片折叠使得
是圆上一个动点,把纸片折叠使得![]() 与
与![]() 重合,然后抹平纸片,折痕为
重合,然后抹平纸片,折痕为![]() ,设
,设![]() 与半径
与半径![]() 的交点为
的交点为![]() ,当
,当![]() 在圆上运动时,则
在圆上运动时,则![]() 点的轨迹为曲线
点的轨迹为曲线![]() ,以
,以![]() 所在直线
所在直线![]() 为轴,
为轴, ![]() 的中垂线为
的中垂线为![]() 轴建立平面直角坐标系,如图.
轴建立平面直角坐标系,如图.
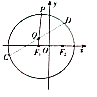
(1)求曲线![]() 的方程;
的方程;
(2)曲线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
, ![]() (
(![]() 在
在![]() 左侧),与
左侧),与![]() 轴不重合的动直线
轴不重合的动直线![]() 过点
过点![]() 且与
且与![]() 交于
交于![]() 、
、![]() 两点(其中
两点(其中![]() 在
在![]() 轴上方),设直线
轴上方),设直线![]() 、
、![]() 交于点
交于点![]() ,求证:动点
,求证:动点![]() 恒在定直线
恒在定直线![]() 上,并求
上,并求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙二人做射击游戏,甲、乙射击击中与否是相互独立事件.规则如下:若射击一次击中,则原射击人继续射击;若射击一次不中,就由对方接替射击.已知甲、乙二人射击一次击中的概率均为![]() ,且第一次由甲开始射击.①求前3次射击中甲恰好击中2次的概率____________;②求第4次由甲射击的概率________.
,且第一次由甲开始射击.①求前3次射击中甲恰好击中2次的概率____________;②求第4次由甲射击的概率________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com