
【题目】已知命题p:指数函数![]() 在R上是单调减函数;命题q:关于x的方程
在R上是单调减函数;命题q:关于x的方程![]() 有实根,
有实根,
(1)若p为真,求a的范围
(2)若q为真,求![]() 的范围
的范围
(3)若p或q为真,p且q为假,求实数a的范围.
科目:高中数学 来源: 题型:
【题目】为践行“绿水青山就是金山银山”的国家发展战略,我市对某辖区内畜牧、化工、煤炭三类行业共200个单位的生态环境治理成效进行了考核评估,考评分数达到85分及其以上的单位被称为“![]() 类”环保单位,未达到85分的单位被称为“
类”环保单位,未达到85分的单位被称为“![]() 类”环保单位.现通过分层抽样的方法确定了这三类行业共20个单位进行调研,统计考评分数如下:
类”环保单位.现通过分层抽样的方法确定了这三类行业共20个单位进行调研,统计考评分数如下:
畜牧类行业:85,92,77,81,89,87
化工类行业:79,77,90,85,83,91
煤炭类行业:87,89,76,84,75,94,90,88
(1)计算该辖区这三类行业中每类行业的单位个数;
(2)若从畜牧类行业这六个单位中,再随机选取两个单位进行生产效益调查,求选出的这两个单位中既有“![]() 类”环保单位,又有“
类”环保单位,又有“![]() 类”环保单位的概率.
类”环保单位的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,其中
,其中![]() 是数列
是数列![]() 的前
的前![]() 项和.
项和.
(1)若数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,求数列
的等比数列,求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)在(2)的条件下,设![]() ,求证:数列
,求证:数列![]() 中的任意一项总可以表示成该数列其他两项之积.
中的任意一项总可以表示成该数列其他两项之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车生产企业上年度生产一品牌汽车的投入成本为10万元/辆,出厂价为14万元/辆,年销售量为![]() 辆.本年度为适应市场需求,计划提高产品档次,适当增加投入成本,若每辆车投入成本增加的比例为
辆.本年度为适应市场需求,计划提高产品档次,适当增加投入成本,若每辆车投入成本增加的比例为![]() (0<
(0<![]() <1),则出厂价相应提高的比例为0.6
<1),则出厂价相应提高的比例为0.6![]() ,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.
,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.
(1)若年销售量增加的比例为0.5![]() ,为使本年度的年利润比上年度有所增加,则投入成本增加的比例
,为使本年度的年利润比上年度有所增加,则投入成本增加的比例![]() 应在什么范围内?
应在什么范围内?
(2)若年销售量关于![]() 的函数为
的函数为![]() 为常数),则当
为常数),则当![]() 为何值时,本年度的年利润最大?
为何值时,本年度的年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线 (
(![]() 为参数),曲线
为参数),曲线![]() (
(![]() 为参数).
为参数).
(1)设![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() ;
;
(2)若把曲线![]() 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的![]() 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,设点
,设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最大时,点P的坐标.
的距离的最大时,点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 为等边三角形,且垂直于底面
为等边三角形,且垂直于底面![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)已知点![]() 在棱
在棱![]() 上且
上且![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在学习强国活动中,某市图书馆的科技类图书和时政类图书是市民借阅的热门图书.为了丰富图书资源,现对已借阅了科技类图书的市民(以下简称为“问卷市民”)进行随机问卷调查,若不借阅时政类图书记1分,若借阅时政类图书记2分,每位市民选择是否借阅时政类图书的概率均为![]() ,市民之间选择意愿相互独立.
,市民之间选择意愿相互独立.
(1)从问卷市民中随机抽取4人,记总得分为随机变量![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)(i)若从问卷市民中随机抽取![]() 人,记总分恰为
人,记总分恰为![]() 分的概率为
分的概率为![]() ,求数列
,求数列![]() 的前10项和;
的前10项和;
(ⅱ)在对所有问卷市民进行随机问卷调查过程中,记已调查过的累计得分恰为![]() 分的概率为
分的概率为![]() (比如:
(比如:![]() 表示累计得分为1分的概率,
表示累计得分为1分的概率,![]() 表示累计得分为2分的概率,
表示累计得分为2分的概率,![]() ),试探求
),试探求![]() 与
与![]() 之间的关系,并求数列
之间的关系,并求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为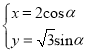 (
(![]() 为参数),在同一平面直角坐标系中,将曲线
为参数),在同一平面直角坐标系中,将曲线![]() 上的点按坐标变换
上的点按坐标变换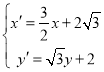 得到曲线
得到曲线![]() ,以原点为极点、
,以原点为极点、![]() 轴的正半轴为极轴,建立极坐标系.
轴的正半轴为极轴,建立极坐标系.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,与曲线
两点,与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com