
| A. | -3 | B. | -2 | C. | 2 | D. | 3 |
分析 由条件利用两角差的余弦公式求得cosα=-$\frac{3}{5}$,可得sinα的值,再利用半角公式求得tan$\frac{α}{2}$的值.
解答 解:α是第三象限,cos(α+β)cosβ+sin(α+β)sinβ=cos[(α+β)-β]=cosα=-$\frac{3}{5}$,
∴sinα=-$\sqrt{{1-cos}^{2}α}$=-$\frac{4}{5}$,
则tan$\frac{α}{2}$=$\frac{1-cosα}{sinα}$=$\frac{1+\frac{3}{5}}{-\frac{4}{5}}$=-2,
故选:B.
点评 本题主要考查两角和差的余弦公式、同角三角函数的基本关系、半角公式的应用,属于基础题.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,$±\sqrt{k}$) | B. | (0,$±\sqrt{2k}$) | C. | (0,$±\sqrt{-k}$) | D. | (0,$±\sqrt{-2k}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 焦点在X轴上的椭圆 | B. | 焦点在Y轴上的椭圆 | ||
| C. | 焦点在X轴上的双曲线 | D. | 焦点在Y轴上的双曲线 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
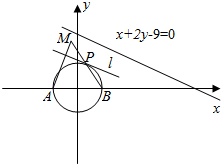 已知圆C:x2+y2=1与x轴的两个交点分别为A,B(由左到右),P为C上的动点,l过点P且与C相切,过点A作l的垂线且与直线BP交于点M,则点M到直线x+2y-9=0的距离的最大值是$2\sqrt{5}+2$.
已知圆C:x2+y2=1与x轴的两个交点分别为A,B(由左到右),P为C上的动点,l过点P且与C相切,过点A作l的垂线且与直线BP交于点M,则点M到直线x+2y-9=0的距离的最大值是$2\sqrt{5}+2$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com