
分析 (1)利用点到直线的距离公式求出半径r,从而求得圆O的方程.
(2)用点斜式设出MN的方程为y=2x+b,由条件求出圆心O到直线MN的距离,即可得到MN的方程.
(3)由题意可得|PA|•|PB|=|PO|2 ,设点P(x,y),代入化简可得x2=y2+9.由点P在圆内可得 x2+y2<18,可得0≤2y2<9.化简$\overrightarrow{PA}•$$\overrightarrow{PB}$=2y2-9,从而求$\overrightarrow{PA}•$$\overrightarrow{PB}$的取值范围.
解答 解:(1)圆F的方程为x2+y2-2x-2y-6=0,可化为(x-1)2+(y-1)2=8
∵圆F的方程为x2+y2-2x-2y-6=0,以坐标原点O为圆心的圆O与圆F相切,
∴圆O的半径r=$\sqrt{2}$或3$\sqrt{2}$,故圆O的方程为x2+y2=2或x2+y2=18.
(2)∵圆O上有两点M、N关于直线x+2y=0对称,
∴MN的斜率等于直线x+2y=0斜率的负倒数,等于2,
设MN的方程为y=2x+b,即2x-y+b=0.
由弦长公式可得,圆心O到直线MN的距离等于$\sqrt{18-3}$=$\sqrt{15}$,
设直线MN的方程为2x-y+b=0,则$\frac{|b|}{\sqrt{5}}$=$\sqrt{15}$,∴b=±5$\sqrt{3}$,
∴直线MN的方程为2x-y±5$\sqrt{3}$=0;
(3)不妨设A(x1,0),B(x2,0),x1<x2.由x2=18即得A(-3$\sqrt{2}$,0),B(3$\sqrt{2}$,0).
设P(x,y),
由|$\overrightarrow{PA}$|,|$\overrightarrow{PO}$|,|$\overrightarrow{PB}$|成等比数列,两边平方,可得(x2+y2+18)2-72x2=(x2+y2)2,
化简整理可得,x2-y2=9.
$\overrightarrow{PA}•$$\overrightarrow{PB}$=x2-18+y2=2y2-9.
由于点P在圆O内,故$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}<18}\\{{x}^{2}-{y}^{2}=9}\end{array}\right.$
由此得0≤2y2<9.
所以$\overrightarrow{PA}•$$\overrightarrow{PB}$的取值范围为[-9,0).
点评 本题主要考查等比数列的定义和性质,直线和圆的位置关系,两个向量的数量积的定义,属于中档题.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:解答题
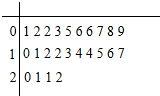 为调查了解某药物使用后病人的康复时间,从1000个使用该药的病人的康复时间中抽取了24个样本,数据如下图中的茎叶图(单位:周).专家指出康复时间在7周之内(含7周)是快效时间.
为调查了解某药物使用后病人的康复时间,从1000个使用该药的病人的康复时间中抽取了24个样本,数据如下图中的茎叶图(单位:周).专家指出康复时间在7周之内(含7周)是快效时间.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
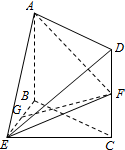 如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BEC,BE⊥EC,AB=BE=EC=2,G是线段BE的中点,点F在线段CD上且GF∥平面ADE.
如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BEC,BE⊥EC,AB=BE=EC=2,G是线段BE的中点,点F在线段CD上且GF∥平面ADE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com