
【题目】如图,在平面直角坐标系xoy中,A为以原点O为圆心的单位圆O与x正半轴的交点,在圆心角为 ![]() 的扇形AOB的弧AB上任取一点 P,作 PN⊥OA于N,连结PO,记∠PON=θ.
的扇形AOB的弧AB上任取一点 P,作 PN⊥OA于N,连结PO,记∠PON=θ. 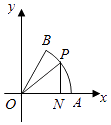
(1)设△PON的面积为y,使y取得最大值时的点P记为E,点N记为F,求此时 ![]() 的值;
的值;
(2)求k=a| ![]() ||
|| ![]() |+
|+ ![]() (a∈R,E 是在(1)条件下的点 E)的值域.
(a∈R,E 是在(1)条件下的点 E)的值域.
【答案】
(1)解:ON=cosθ,PN=sinθ,
∴y= ![]() cosθsinθ=
cosθsinθ= ![]() sin2θ,
sin2θ,
∵0 ![]() ,
,
∴当 ![]() 时,y取得最大值,此时E(
时,y取得最大值,此时E( ![]() ,
, ![]() ),F(
),F( ![]() ,0),
,0),
∴ ![]() =
= ![]() .
.
(2)解: ![]() =(cosθ,sinθ),
=(cosθ,sinθ), ![]() =(
=( ![]() ,
, ![]() ),
),
∴ ![]() =
= ![]() cosθ+
cosθ+ ![]() sinθ=
sinθ= ![]() (sinθ+cosθ),
(sinθ+cosθ),
∴k=asinθcosθ+sinθ+cosθ,
令sinθ+cosθ= ![]() sin(
sin( ![]() )=t,则sinθcosθ=
)=t,则sinθcosθ= ![]() ,
,
∵0 ![]() ,∴
,∴ ![]() ≤
≤ ![]() ,
,
∴1<t ![]() ,
,
∴k=a ![]() +t=
+t= ![]() ,
,
令f(t)= ![]() ,
,
①若a=0,则f(t)=t,∴f(t)的值域为(1, ![]() ];
];
②若a>0,则f(t)的对称轴为直线x=﹣ ![]() <0,
<0,
∴f(t)在(1, ![]() ]上单调递增,
]上单调递增,
∴f(1)<f(t)≤f( ![]() ),即f(t)的值域为(1,
),即f(t)的值域为(1, ![]() +
+ ![]() ];
];
③若a<0,则f(t)的图象开口向下,
若﹣ ![]() ≤1,即a≤﹣1时,f(t)在(1,
≤1,即a≤﹣1时,f(t)在(1, ![]() ]上单调递减,
]上单调递减,
∴f(t)的值域为[ ![]() +
+ ![]() ,1);
,1);
若﹣ ![]() ≥
≥ ![]() ,即﹣
,即﹣ ![]() ≤a<0时,f(t)在(1,
≤a<0时,f(t)在(1, ![]() ]上单调递增,
]上单调递增,
∴f(t)的值域为(1, ![]() +
+ ![]() ];
];
若1<﹣ ![]() ,即﹣1
,即﹣1 ![]() 时,f(t)在(1,
时,f(t)在(1, ![]() ]上先增后减,
]上先增后减,
∴f(t)的最大值为f(﹣ ![]() )=
)= ![]() ,
,
若1 ![]() <
< ![]() ,即﹣1<a<2﹣2
,即﹣1<a<2﹣2 ![]() 时,则f(t)的最小值为f(
时,则f(t)的最小值为f( ![]() )=
)= ![]() ,
,
若 ![]() ≤﹣
≤﹣ ![]() ,即2﹣2
,即2﹣2 ![]() ≤a<﹣
≤a<﹣ ![]() 则f(t)的最小值为f(1)=1,
则f(t)的最小值为f(1)=1,
综上,当a=0时,f(t)的值域为(1, ![]() ];
];
当a≤﹣1时,k的值域是[ ![]() +
+ ![]() ,1);
,1);
当a>﹣ ![]() 且a≠0时,k的值域是(1,
且a≠0时,k的值域是(1, ![]() +
+ ![]() ];
];
﹣1<a<2﹣2 ![]() 时,k的值域是[
时,k的值域是[ ![]() ,
, ![]() ];
];
当2﹣2 ![]() ≤a<﹣
≤a<﹣ ![]() 时,k的值域是(1,
时,k的值域是(1, ![]() ].
].
【解析】(1)用θ表示出PN,ON,得出y关于θ的函数,利用正弦函数的性质得出y最大时对应的θ值,从而求出E,F的坐标,再计算 ![]() ;(2)设sinθ+cosθ=t,得出k关于t的函数,讨论a的取值与函数单调性,得出k的值域.
;(2)设sinθ+cosθ=t,得出k关于t的函数,讨论a的取值与函数单调性,得出k的值域.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4cosxsin(x+ ![]() )﹣1, (Ⅰ)求f(x)的单调递增区间
)﹣1, (Ⅰ)求f(x)的单调递增区间
(Ⅱ)若sin2x+af(x+ ![]() )+1>6cos4x对任意x∈(﹣
)+1>6cos4x对任意x∈(﹣ ![]() ,
, ![]() )恒成立,求实数a的取值范围.
)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校高三1200名学生中随机抽取40名,将他们一次数学模拟成绩绘制成频率分布直方图(如图)(满分为150分,成绩均为不低于80分整数),分为7段:[80,90),[90,100),[100,110),[110,120),[120,130),[130,140),[140,150]. 
(1)求图中的实数a的值,并估计该高三学生这次成绩在120分以上的人数;
(2)在随机抽取的40名学生中,从成绩在[90,100)与[140,150]两个分数段内随机抽取两名学生,求这两名学生的成绩之差的绝对值标不大于10的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥A﹣BCDE,其中AB=BC=AC=BE=1,CD=2,CD⊥面ABC,BE∥CD,F为AD的中点.
(Ⅰ)求证:EF∥面ABC;
(Ⅱ)求证:平面ADE⊥平面ACD;
(Ⅲ)求四棱锥A﹣BCDE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答题。
(1)如图,证明命题“a是平面π内的一条直线,b是π外的一条直线(b不垂直于π),c是直线b在π上的投影,若a⊥b,则a⊥c”为真.
(2)写出上述命题的逆命题,并判断其真假(不需要证明) 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|ax﹣1|﹣(a﹣1)x
(1)当a= ![]() 时,满足不等式f(x)>1的x的取值范围为;
时,满足不等式f(x)>1的x的取值范围为;
(2)若函数f(x)的图象与x轴没有交点,则实数a的取值范围为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一条光线从点(﹣2,﹣3)射出,经y轴反射后与圆(x+3)2+(y﹣2)2=1相切,则反射光线所在直线的斜率为( )
A.﹣ ![]() 或﹣
或﹣ ![]()
B.﹣ ![]() 或﹣
或﹣ ![]()
C.﹣ ![]() 或﹣
或﹣ ![]()
D.﹣ ![]() 或﹣
或﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车是城市慢行系统的一种模式创新,对于解决民众出行“最后一公里”的问题特别见效,由于停取方便、租用价格低廉,各色共享单车受到人们的热捧.某自行车厂为共享单车公司生产新样式的单车,已知生产新样式单车的固定成本为20000元,每生产一件新样式单车需要增加投入100元.根据初步测算,自行车厂的总收益(单位:元)满足分段函数h(x),其中  x是新样式单车的月产量(单位:件),利润=总收益﹣总成本.
x是新样式单车的月产量(单位:件),利润=总收益﹣总成本.
(1)试将自行车厂的利润y元表示为月产量x的函数;
(2)当月产量为多少件时自行车厂的利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知圆O:x2+y2=1,O1:(x﹣4)2+y2=4,动点P在直线x+ ![]() y+b=0上,过P分别作圆O,O1的切线,切点分别为A,B,若满足PB=2PA的点P有且只有两个,则实数b的取值范围是 .
y+b=0上,过P分别作圆O,O1的切线,切点分别为A,B,若满足PB=2PA的点P有且只有两个,则实数b的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com