
【题目】已知函数f(x)是定义在D上的函数,若存在区间[m,n]D及正实数k,使函数f(x)在[m,n]上的值域恰为[km,kn],则称函数f(x)是k型函数.给出下列说法:
①f(x)=3﹣ ![]() 不可能是k型函数;
不可能是k型函数;
②若函数f(x)= ![]() (a≠0)是1型函数,则n﹣m的最大值为
(a≠0)是1型函数,则n﹣m的最大值为 ![]() ;
;
③若函数f(x)=﹣ ![]() x2+x是3型函数,则m=﹣4,n=0.
x2+x是3型函数,则m=﹣4,n=0.
其中正确说法个数为( )
A.0
B.1
C.2
D.3
【答案】C
【解析】分析:解答:解:对于①,f(x)的定义域是{x|x≠0},且f(2)=3﹣ ![]() =1,f(4)=3﹣
=1,f(4)=3﹣ ![]() =2,
=2,
∴f(x)在[2,4]上的值域是[1,2],
∴f(x)是 ![]() 型函数,∴命题错误;
型函数,∴命题错误;
对于②,y= ![]() (a≠0)是1型函数,
(a≠0)是1型函数,
即(a2+a)x﹣1=a2x2 , ∴a2x2﹣(a2+a)x+1=0,
∴方程的两根之差x1﹣x2= ![]() =
= ![]() ≤
≤ ![]() ,
,
即n﹣m的最大值为 ![]() ;∴命题正确;
;∴命题正确;
对于③,y=﹣ ![]() x2+x是3型函数,
x2+x是3型函数,
即﹣ ![]() x2+x=3x,解得x=0,或x=﹣4,
x2+x=3x,解得x=0,或x=﹣4,
∴m=﹣4,n=0;∴命题正确;
综上,正确的命题是②③.
故选:C.
【考点精析】关于本题考查的函数的定义域及其求法和函数的值域,需要了解求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的才能得出正确答案.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的才能得出正确答案.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】2017 年省内某事业单位面向社会公开招骋工作人员,为保证公平竞争,报名者需要参加笔试和面试两部分,且要求笔试成绩必须大于或等于![]() 分的才有资格参加面试,
分的才有资格参加面试, ![]() 分以下(不含
分以下(不含![]() 分)则被淘汰,现有
分)则被淘汰,现有![]() 名竞骋者参加笔试,参加笔试的成绩按区间
名竞骋者参加笔试,参加笔试的成绩按区间![]() 分段,其频率分布直方图如图所示(频率分布直方图有污损),但是知道参加面试的人数为
分段,其频率分布直方图如图所示(频率分布直方图有污损),但是知道参加面试的人数为![]() ,且笔试成绩在
,且笔试成绩在![]() 的人数为
的人数为![]() .
.

(1)根据频率分布直方图,估算竞骋者参加笔试的平均成绩;
(2)若在面试过程中每人最多有![]() 次选题答题的机会,累计答对
次选题答题的机会,累计答对![]() 题或答错
题或答错![]() 题, 答对
题, 答对![]() 题者方可参加复赛,已知面试者甲答对每一个问题的概率都相同,并且相互之间没有影响,若他连续三次答题中答对一次的概率为
题者方可参加复赛,已知面试者甲答对每一个问题的概率都相同,并且相互之间没有影响,若他连续三次答题中答对一次的概率为![]() ,求面试者甲答题个数
,求面试者甲答题个数![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2013江苏,理17】如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4.设圆C的半径为1,圆心在l上.
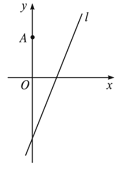
(1)若圆心C也在直线y=x-1上,过点A作圆C的切线,求切线的方程;
(2)若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.二进制数11010(2)化为八进制数为42(8)
B.若扇形圆心角为2弧度,且扇形弧所对的弦长为2,则这个扇形的面积为 ![]()
C.用秦九韶算法计算多项式f(x)=3x6+5x4+6x3﹣4x﹣5当x=3时的值时,v1=3v0+5=32
D.正切函数在定义域内为单调增函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD,PD⊥底面ABCD,且底面ABCD是边长为2的正方形,M、N分别为PB、PC的中点. 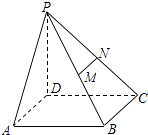
(1)证明:MN∥平面PAD;
(2)若PA与平面ABCD所成的角为45°,求四棱锥P﹣ABCD的体积V.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方体ABCD﹣A1B1C1D1的棱长为1,BD∩AC=0,M是线段D1O上的动点,过点M做平面ACD1的垂线交平面A1B1C1D1于点N,则点N到点A距离的最小值为( ) 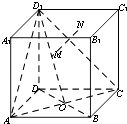
A.![]()
B.![]()
C.![]()
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 与圆
与圆![]() :
: ![]() 相切,且与圆
相切,且与圆![]() :
: ![]() 相内切,记圆心
相内切,记圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .设
.设![]() 为曲线
为曲线![]() 上的一个不在
上的一个不在![]() 轴上的动点,
轴上的动点, ![]() 为坐标原点,过点
为坐标原点,过点![]() 作
作![]() 的平行线交曲线
的平行线交曲线![]() 于
于![]() ,
, ![]() 两个不同的点.
两个不同的点.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)试探究![]() 和
和![]() 的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
(Ⅲ)记![]() 的面积为
的面积为![]() ,
, ![]() 的面积为
的面积为![]() ,令
,令![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com