Question

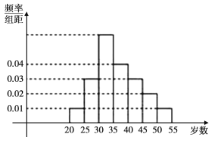
【题目】某中学利用周末组织教职员工进行了一次秋季登山健身的活动，有Ⅳ人参加，现将所有参加者按年龄情况分为，，，，，，等七组，其频率分布直方图如图所示，已知这组的参加者是6人．

（1）已知和这两组各有2名数学教师，现从这两个组中各选取2人担任接待工作，设两组的选择互不影响，求两组选出的人中恰有1名数学老师的概率；

（2）组织者从这组的参加者（其中共有4名女教师，其余全为男教师）中随机选取3名担任后勤保障工作，其中女教师的人数为，求的分布列和均值．

Answer 1

【答案】（1）；（2）见解析.

【解析】

（1）根据频率分布直方图，先得到年龄在之间的概率，再由这组的参加者是6人，求得参加的总人数.然后分别求得年龄在和之间的人数，然后利用古典概型的概率求解.

（2）先得到年龄在的人数，根据有4名女教师，则的可能取值为：1，2，3，然后求得相应的概率，列出分布列再求期望.

（1）因为年龄在之间的概率为，

又这组的参加者是6人，

所以参加的总人数为，

所以年龄在之间的人数为，

年龄在之间的人数为，

所以两组选出的人中恰有1名数学老师的概率.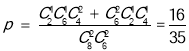

（2）年龄在的人数为：，从中随机选取3名担任后勤保障工作，其中女教师的人数为，的可能取值为：1，2，3

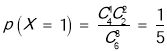
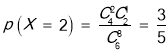
分布列为：

X	1	2	3
p

均值 .