
(本题满分12分)已知函数y=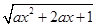 的定义域为R,解关于x的不等式
的定义域为R,解关于x的不等式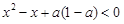
当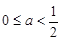 时,
时,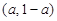 ;当
;当 时,Ф;当
时,Ф;当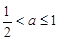 时,
时,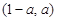 .
.
【解析】
试题分析:由条件可得0≤a≤1,原不等式可化为(x-a)[x-(1-a)]>0,分0≤a<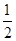 、a=
、a=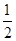 、
、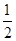 <a≤1三种情况,分别求出不等式的解集.
<a≤1三种情况,分别求出不等式的解集.
解:∵函数y=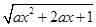 的定义域为R,∴
的定义域为R,∴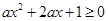 恒成立. …1分
恒成立. …1分
当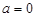 时,
时,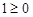 ,不等式恒成立;当
,不等式恒成立;当 时,则
时,则
解得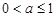 .综上,
.综上,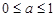 ………………………4分
………………………4分
由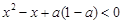 得
得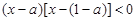 .……6分
.……6分
∵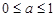 ,
,
∴(1)当 ,即
,即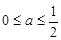 时,
时,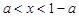 ;
;
(2)当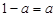 ,即
,即 时,
时, ,不等式无解;
,不等式无解;
(3)当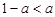 ,即
,即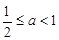 时,
时,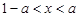 .………………………………10分
.………………………………10分
∴原不等式的解集为:当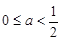 时,
时,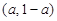 ;当
;当 时,Ф;当
时,Ф;当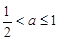 时,
时,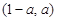 .
……………………12分
.
……………………12分
考点:本试题主要考查了二元一次不等式的解法,函数的恒成立问题,体现了分类讨论的数学思想,属于中档题.
点评:解决该试题的关键是由条件可得0≤a≤1,对于参数a,分0≤a<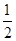 、a=
、a=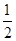 、
、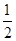 <a≤1三种情况,分别求出不等式的解集.
<a≤1三种情况,分别求出不等式的解集.


科目:高中数学 来源: 题型:
| π | 2 |
查看答案和解析>>
科目:高中数学 来源:安徽省合肥一中、六中、一六八中学2010-2011学年高二下学期期末联考数学(理 题型:解答题
(本题满分12分)已知△ 的三个内角
的三个内角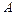 、
、 、
、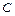 所对的边分别为
所对的边分别为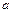 、
、 、
、 .
.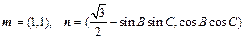 ,且
,且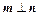 .(1)求
.(1)求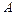 的大小;(2)若
的大小;(2)若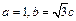 .求
.求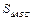 .
.
查看答案和解析>>
科目:高中数学 来源:2011届本溪县高二暑期补课阶段考试数学卷 题型:解答题
(本题满分12分)已知各项均为正数的数列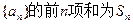 ,
,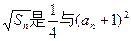 的等比中项。
的等比中项。
(1)求证:数列 是等差数列;(2)若
是等差数列;(2)若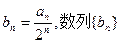 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省揭阳市高三调研检测数学理卷 题型:解答题
(本题满分12分)
已知椭圆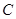 :
: 的长轴长是短轴长的
的长轴长是短轴长的 倍,
倍,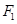 ,
,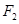 是它的左,右焦点.
是它的左,右焦点.
(1)若 ,且
,且 ,
,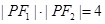 ,求
,求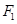 、
、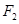 的坐标;
的坐标;
(2)在(1)的条件下,过动点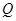 作以
作以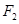 为圆心、以1为半径的圆的切线
为圆心、以1为半径的圆的切线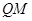 (
(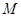 是切点),且使
是切点),且使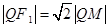 ,求动点
,求动点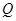 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源:2010年辽宁省高二上学期10月月考理科数学卷 题型:解答题
(本题满分12分)已知椭圆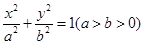 的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量
的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量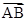 与
与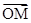 是共线向量
是共线向量
(1)求椭圆的离心率
(2)设Q是椭圆上任意一点,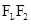 分别是左右焦点,求
分别是左右焦点,求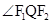 的取值范围
的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com