Question

）设点C为曲线y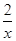＝(x>0)上任一点，以点C为圆心的圆与x轴交于点E、A，与y轴交于点E、B.

(1)证明：多边形EACB的面积是定值，并求这个定值；

(2)设直线y＝－2x＋4与圆C交于点M，N，若|EM|＝|EN|，求圆C的方程．

 

Answer 1

【答案】

（1）见解析；（2）(x－2)²＋(y－1)²＝5.

【解析】(1)可直接确定点E为原点，所以设圆心C，然后根据半径长度为|OC|，即可写出圆的标准方程 ,然后再求四边形的面积看是否是定值即可。

（2）根据圆的几何性质可知CE所在直线与直线y=-2x+4垂直，所以根据斜率积为-1，即可求出t的值，进而确定圆的方程。

解：(1)证明：设点C (t>0)，因为以点C为圆心的圆与x轴交于点E、A，与y轴交于点E、B.

所以，点E是直角坐标系原点，即E(0,0)．

于是圆C的方程是(x－t)²＋²＝t²＋.

则A(2t,0)，B.

由|CE|＝|CA|＝|CB|知，圆心C在Rt△AEB的斜边AB上，于是多边形EACB为Rt△AEB，

其面积S＝|EA|·|EB|＝×2t×＝4.

所以多边形EACB的面积是定值，这个定值是4.

(2)若|EM|＝|EN|，则E在MN的垂直平分线上，即EC是MN的垂直平分线．

因为k_EC＝＝，k_MN＝－2.

所以由k_EC·k_MN＝－1得t＝2.

所以圆C的方程是(x－2)²＋(y－1)²＝5.