
 如图,矩形ABCD与矩形ADEF所在的平面互相垂直,将△DEF沿FD翻折,翻折后的点E(记为点P)恰好落在BC上,设AB=1,FA=x(x>1),AD=y,则以下结论正确的是( )
如图,矩形ABCD与矩形ADEF所在的平面互相垂直,将△DEF沿FD翻折,翻折后的点E(记为点P)恰好落在BC上,设AB=1,FA=x(x>1),AD=y,则以下结论正确的是( )| A. | 当x=2时,y有最小值$\frac{4\sqrt{3}}{3}$ | B. | 当x=2时,有最大值$\frac{4\sqrt{3}}{3}$ | ||
| C. | 当x=$\sqrt{2}$时,y有最小值2 | D. | 当x=$\sqrt{2}$时,y有最大值2 |
分析 由已知得FE=FP=AD=BC=y,AB=DC=1,FA=DE=DP=x,从而PC=$\sqrt{{x}^{2}-1}$,AP=$\sqrt{{y}^{2}-{x}^{2}}$,BP=$\sqrt{{y}^{2}-{x}^{2}-1}$,进而得到y2=$\frac{{x}^{4}}{{x}^{2}-1}$=$\frac{1}{\frac{1}{{x}^{2}}-\frac{1}{{x}^{4}}}$,由此利用换元法及二次函数性质能求出结果.
解答 解:∵矩形ABCD与矩形ADEF所在的平面互相垂直,
AB=1,FA=x(x>1),AD=y,
∴FE=FP=AD=BC=y,AB=DC=1,FA=DE=DP=x
在Rt△DCP中,PC=$\sqrt{{x}^{2}-1}$,
在Rt△FAP中,AP=$\sqrt{{y}^{2}-{x}^{2}}$,
在Rt△ABP中,BP=$\sqrt{{y}^{2}-{x}^{2}-1}$,
∵BC=BP+PC=$\sqrt{{y}^{2}-{x}^{2}-1}$+$\sqrt{{x}^{2}-1}$=y
整理得y2=$\frac{{x}^{4}}{{x}^{2}-1}$=$\frac{1}{\frac{1}{{x}^{2}}-\frac{1}{{x}^{4}}}$,令t=$\frac{1}{{x}^{2}}$
则y2=$\frac{1}{-{t}^{2}+t}$,
则当t=$\frac{1}{2}$,即x=$\sqrt{2}$时,y取最小值.
故选:C.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间位置关系、换元法、二次函数性质的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,PA=PB=AD=2,四边形ABCD满足AB⊥AD,BC∥AD且BC=4,点M为PC的中点,点E为BC边上的点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,PA=PB=AD=2,四边形ABCD满足AB⊥AD,BC∥AD且BC=4,点M为PC的中点,点E为BC边上的点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
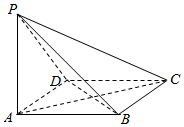 如图,四棱锥P-ABCD中,底面ABCD是平行四边形,且PA⊥平面ABCD,PA=AB=AD=2,∠BAD=60°.
如图,四棱锥P-ABCD中,底面ABCD是平行四边形,且PA⊥平面ABCD,PA=AB=AD=2,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
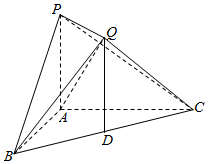 如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=1,AB=AC=$\sqrt{2}$,D为BC的中点,过点D作DQ∥AP,且DQ=1,连结QB,QC,QP.
如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=1,AB=AC=$\sqrt{2}$,D为BC的中点,过点D作DQ∥AP,且DQ=1,连结QB,QC,QP.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB为圆O的直径,点C为圆O上的一点,且BC=$\sqrt{3}$AC,点D为线段AB上一点,且AD=$\frac{1}{3}$DB.PD垂直于圆O所在的平面.
如图,AB为圆O的直径,点C为圆O上的一点,且BC=$\sqrt{3}$AC,点D为线段AB上一点,且AD=$\frac{1}{3}$DB.PD垂直于圆O所在的平面.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com