
【题目】设数列{an}的前n项和为Sn , 已知S2=6,an+1=4Sn+1,n∈N* .
(1)求通项an;
(2)设bn=an﹣n﹣4,求数列{|bn|}的前n项和Tn .
【答案】
(1)解:∵an+1=4Sn+1,①
∴当n≥2时,an=4Sn﹣1+1,②
由①﹣②,得
an+1﹣an=4(Sn﹣Sn﹣1)=4an(n≥2),
∴当n≥2时,an+1=5an(n≥2),
∴ ![]() =5.
=5.
∵S2=6,an+1=4Sn+1,n∈N*.
∴ ![]() ,
,
解得 ![]() ,
,
∴ ![]() =5,
=5,
∴数列{an}是首项a1=1,公比为5的等边数列,
∴an=5n﹣1;
(2)解:由题意知|bn|=|5n﹣1﹣n﹣4|,n∈N*.
易知,当n≤2时,5n﹣1<n+4;当n≥3时,5n﹣1>n+4.
∴当n≤2时,|bn|=n+4﹣5n﹣1;
当n≥3时,|bn|=5n﹣1﹣(n+4),
∴T1=b1=4,T2=b1+b2=5.
当n≥3时,Tn=T2+b2+b3+…+bn
=5+[52﹣(3+4)+[52﹣(4+4)]+…+[5n﹣1﹣(n+4)]
=5+(52+53+…+5n﹣1)﹣[(3+4)+(4+4)+…+(n+4)]
=5+ ![]() ﹣
﹣ ![]()
= ![]() .
.
又∵T1=4不满足上式,T2=5满足上式,
∴Tn= 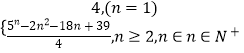
【解析】(1)利用已知条件和变形等式an=4Sn﹣1+1推知数列{an}是等边数列,根据等比数列的通项公式进行解答;(2)利用(1)中的通项公式推知{|bn|}的通项公式.然后由分组求和法来求数列{|bn|}的前n项和Tn .
【考点精析】根据题目的已知条件,利用数列的前n项和和数列的通项公式的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系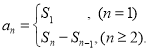 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0),四点P1(1,1),P2(0,1),P3(﹣1,
=1(a>b>0),四点P1(1,1),P2(0,1),P3(﹣1, ![]() ),P4(1,
),P4(1, ![]() )中恰有三点在椭圆C上.(12分)
)中恰有三点在椭圆C上.(12分)
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为﹣1,证明:l过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直三棱柱ABC﹣A1B1C1中,∠ABC=120°,AB=2,BC=CC1=1,则异面直线AB1与BC1所成角的余弦值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)是定义在R上的奇函数,对任意的x∈R,满足f(x+1)+f(x)=0,且当0<x<1时,f(x)=2x , 则f(﹣ ![]() )+f(4)= .
)+f(4)= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】考察下列命题:其中正确的命题有 ( )
(1)掷两枚硬币,可能出现“两个正面”、“两个反面”、“一正一反”3种结果;
(2)某袋中装有大小均匀的三个红球、二个黑球、一个白球,那么每种颜色的球被摸到的可能性相同;(3)从![]() 中任取一数,取到的数小于0与不小于0的可能性相同;
中任取一数,取到的数小于0与不小于0的可能性相同;
(4)分别从3个男同学、4个女同学中各选一个作代表,那么每个同学当选的可能性相同;
(5)5人抽签,甲先抽,乙后抽,那么乙与甲抽到某号中奖签的可能性肯定不同.
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,A,B,C所对的边分别为a,b,c,已知sinC= ![]() .
.
(1)若a+b=5,求△ABC面积的最大值;
(2)若a=2,2sin2A+sinAsinC=sin2C,求b及c的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com