
【题目】设f(x)=1﹣![]() ,求解:(1)f(x)的值域;(2)证明f(x)为R上的增函数. .
,求解:(1)f(x)的值域;(2)证明f(x)为R上的增函数. .
(1)求f(x)的值域;
(2)证明f(x)为R上的增函数.
【答案】
(1)
解:因为2x>0,所以 ,所以﹣1<1﹣ <1,
即f(x)的值域为(﹣1,1);
(2)
解:任取x1、x2,且x1<x2.
则f(x2)﹣f(x1)= = >0
所以f(x2)>f(x1)
所以f(x)为R上的增函数
【解析】分析:(1)因为2x>0,由不等式的性质即可求出1﹣ ![]() 的范围,即f(x)的值域.(2)由怎函数的哦定义,只要任取两个自变量,由做差法比较他们对应函数值的大小即可.
的范围,即f(x)的值域.(2)由怎函数的哦定义,只要任取两个自变量,由做差法比较他们对应函数值的大小即可.
【考点精析】本题主要考查了函数单调性的判断方法的相关知识点,需要掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较才能正确解答此题.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() cos2x﹣
cos2x﹣![]() sinxcosx﹣
sinxcosx﹣![]() sin2x.
sin2x.
(Ⅰ)求函数f(x)取得最大值时x的集合;
(Ⅱ) 设A、B、C为锐角三角形ABC的三个内角,若cosB=![]() ,f(C)=﹣
,f(C)=﹣![]() ,求sinA的值.
,求sinA的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+![]() +alnx.
+alnx.
(Ⅰ)若f(x)在区间[2,3]上单调递增,求实数a的取值范围;
(Ⅱ)设f(x)的导数f’(x )的图象为曲线C ,曲线C 上的不同两点A (x1, y1) ,B (x2,y 2) 所在直线的斜率为k ,求证:当a≤4时,|k|>1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某宾馆有相同标准的床位100张,根据经验,当该宾馆的床价(即每张床每天的租金)不超过10元时,床位可以全部租出,当床价高于10元时,每提高1元,将有3张床位空闲.为了获得较好的效益,该宾馆要给床位定一个合适的价格,条件是:①要方便结账,床价应为1元的整数倍;②该宾馆每日的费用支出为575元,床位出租的收入必须高于支出,而且高出得越多越好.若用x表示床价,用y表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入).
(1)把y表示成x的函数,并求出其定义域;
(2)试确定该宾馆将床位定价为多少时,既符合上面的两个条件,又能使净收入最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]() .
.
(1)判断函数f(x)的奇偶性并证明;
(2)证明f(x)是定义域内的增函数;
(3)解不等式f(1﹣m)+f(1﹣m2)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列两个变量之间的关系哪个不是函数关系( )
A.角度和它的正切值
B.人的右手一柞长和身高
C.正方体的棱长和表面积
D.真空中自由落体运动物体的下落距离和下落时间
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设S,T是R的两个非空子集,如果存在一个从S到T的函数y=f(x)满足:(i)T={f(x)|x∈S};(ii)对任意x1 , x2∈S,当x1<x2时,恒有f(x1)<f(x2),那么称这两个集合“保序同构”,以下集合对不是“保序同构”的是( )
A.A=N* , B=N
B.A={x|﹣1≤x≤3},B={x|x=﹣8或0<x≤10}
C.A={x|0<x<1},B=R
D.A=Z,B=Q
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某品牌手机公司生产某款手机的年固定成本为40万美元,每生产1万部还需另投入16万美元.设公司一年内共生产该款手机x万部并全部销售完,每万部的销售收入为R(x)万美元,且R(x)= 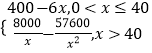 .
.
(1)写出年利润f(x)(万美元)关于年产量x(万部)的函数解析式;
(2)当年产量为多少万部时,公司在该款手机的生产中所获得的利润最大?并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com