
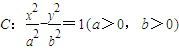 的两条渐近线互相垂直,且C的焦点到其渐近线的距离为
的两条渐近线互相垂直,且C的焦点到其渐近线的距离为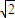 ,过点E(1,0)且倾斜角为锐角的直线l交C于A、B两点.
,过点E(1,0)且倾斜角为锐角的直线l交C于A、B两点. ,求直线l斜率的取值范围.
,求直线l斜率的取值范围.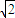 ,求出b,再由两条渐近线互相垂直,求得a=b=
,求出b,再由两条渐近线互相垂直,求得a=b=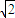 ,从而得到双曲线C的方程.
,从而得到双曲线C的方程.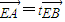 ,得到
,得到 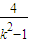 =t+
=t+ +2,由t的范围求出
+2,由t的范围求出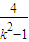 的范围,进而得到k的范围.
的范围,进而得到k的范围.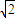 ,
,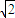 =
=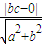 ,b=
,b=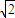 .
.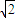 ,
, 得(1-k2)y2+2ky-k2=0,∴△=4k2-4(1-k2)(-k2)>0,
得(1-k2)y2+2ky-k2=0,∴△=4k2-4(1-k2)(-k2)>0,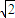 且 k≠1.
且 k≠1.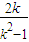 ,y1•y2=
,y1•y2=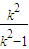 ,
,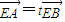 ,∴( x1-1,y1)=t(x2-1,y2),∴y1=ty2.
,∴( x1-1,y1)=t(x2-1,y2),∴y1=ty2.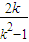 ,t y22=
,t y22=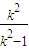 ,消去y2得
,消去y2得 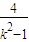 =t+
=t+ +2.
+2.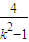 <
<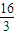 ,∴
,∴ <k2<2. 又0<k<
<k2<2. 又0<k<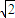 且 k≠1,
且 k≠1,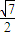 <k<
<k<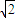 ,
,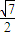 ,
,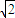 ).
).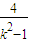 的范围,进而得到k的范围,‘是解题的关键和难点.
的范围,进而得到k的范围,‘是解题的关键和难点. 

科目:高中数学 来源:重庆市高考真题 题型:解答题
 ,0)为右焦点的双曲线C的离心率,
,0)为右焦点的双曲线C的离心率,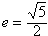 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知双曲线![]() 的一条渐近方程为
的一条渐近方程为![]() ,两条准线的距离为1。
,两条准线的距离为1。
(1)求双曲线的方程;
(2)直线l过坐标原点O且和双曲线交于两点M,N,点P为双曲线上异于M,N的一点,且直线PM,PN的斜率均存在,求kPM?kPN的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com